题目内容
函数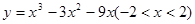 有 ( )
有 ( )
| A.极大值为5,极小值为-27 | B.极大值为5,极小值为-11 |
| C.极大值为5,无极小值 | D.极小值为-27,无极大值 |
C
解析试题分析: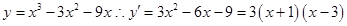 ,令
,令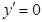 得
得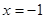 ,当
,当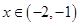 时
时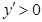 ,当
,当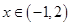 时
时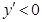 ,所以函数在
,所以函数在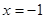 处取得极大值5,无极小值
处取得极大值5,无极小值
考点:函数极值
点评:求函数极值的步骤:1,求函数定义域,2,求函数导数,3,令导数为零得极值点,4判定极值点分成的若干区间内的导数正负从而确定是极大值还是极小值

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
设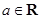 ,函数
,函数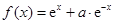 的导函数是
的导函数是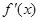 ,且
,且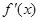 是奇函数.若曲线
是奇函数.若曲线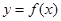 的一条切线的斜率是
的一条切线的斜率是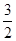 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.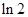 | B.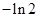 | C.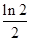 | D.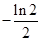 |
已知函数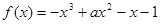 在
在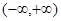 上是单调函数,则实数a的取值范围是( )
上是单调函数,则实数a的取值范围是( )
A.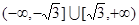 | B.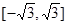 |
C.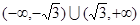 | D.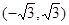 |
若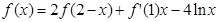 ,则
,则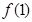 等于( )
等于( )
A.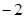 | B.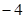 | C.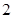 | D.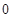 |
设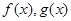 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当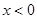 时,
时, ,且
,且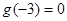 ,则
,则 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
设 ,若函数
,若函数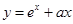 ,
,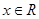 ,有大于零的极值点,则( )
,有大于零的极值点,则( )
A.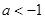 | B.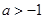 | C.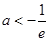 | D.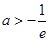 |
函数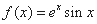 的图象在点
的图象在点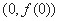 处的切线的倾斜角为
处的切线的倾斜角为
A. | B.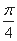 | C.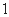 | D.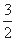 |
若曲线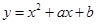 在点
在点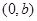 处的切线方程是
处的切线方程是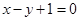 ,则( )
,则( )
A.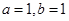 | B.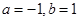 |
C.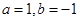 | D.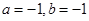 |
若 ,则
,则 等于
等于
| A.2 | B.-2 | C. | D. |