题目内容
已知在△OAB(O为原点)中,| OA |
| OB |
| OA |
| OB |
分析:由已知得|
|=2,|
|=5,则根据
•
=-5,易求两个向量夹角的余弦值,再根据同角三角函数的平方关系,可以得到两个向量夹角(即∠0)的正弦值,代入三角形面积公式,即可求解.
| OA |
| OB |
| OA |
| OB |
解答:解:∵
=(2cosa,2sina),
=(5cosb,5sinb),
∴|
|=2,|
|=5,
又∵
•
=-5,
可得:cos∠O=-
则sin∠O=
=
∴S△AOB=
•|
|•|
|•
=
故答案为:
| OA |
| OB |
∴|
| OA |
| OB |
又∵
| OA |
| OB |
可得:cos∠O=-
| 1 |
| 2 |
则sin∠O=
| 1-cos2∠O |
| ||
| 2 |
∴S△AOB=
| 1 |
| 2 |
| OA |
| OB |
| ||
| 2 |
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:如果已知两边长求三角形面积,一般思路有两种:求出第三边,利用海伦公式进行求解;求出夹角利用S=
absicC求解,关键是要根据已知条件,选择最恰当的方法.
| 1 |
| 2 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
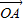 =(2cosa,2sina),
=(2cosa,2sina),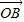 =(5cosb,5sinb),若
=(5cosb,5sinb),若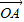 •
•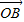 =-5,则S△AOB的值为 .
=-5,则S△AOB的值为 .