题目内容
用数学归纳法证明等式:
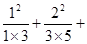 …
…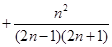 =
=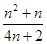
对于一切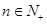 都成立.
都成立.
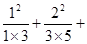 …
…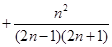 =
=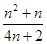
对于一切
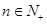 都成立.
都成立.利用数学归纳法。
试题分析:(1)当n=1时,左边=
 ,右边=
,右边=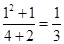 ,等式成立。
,等式成立。(2)假设n=k时,等式成立,即
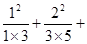 …
…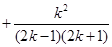 =
= ,
,那么n=k+1时,
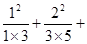 ……
……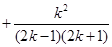

=


=
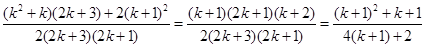 ,
,这就是说,当n=k+1时 等式也成了
故对一切
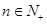 等式都成立。
等式都成立。点评:容易题,利用数学归纳法,可证明与自然数有关的命题,证明过程中,要注意规范写出“两步一结”。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
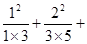 …
…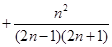 =
=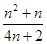
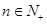 都成立.
都成立. ,右边=
,右边=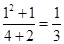 ,等式成立。
,等式成立。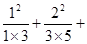 …
…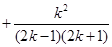 =
= ,
,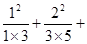 ……
……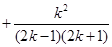



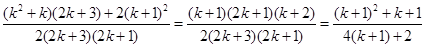 ,
,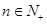 等式都成立。
等式都成立。
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案