题目内容
定义函数y=f(x):对于任意整数m,当实数x 时,有f(x)=m.
时,有f(x)=m.(Ⅰ)设函数的定义域为D,画出函数f(x)在x∈D∩[0,4]上的图象;
(Ⅱ)若数列
 (n∈N*),记Sn=f(a1)+f(a2)+…+f(an),求Sn;
(n∈N*),记Sn=f(a1)+f(a2)+…+f(an),求Sn;(Ⅲ)若等比数列bn的首项是b1=1,公比为q(q>0),又f(b1)+f(b2)+f(b3)=4,求公比q的取值范围.
【答案】分析:(Ⅰ)根据函数y=f(x)的定义,求出函数在区间[0,4]上的解析式,即可画出函数的图象;
(Ⅱ)根据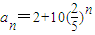 ,可知2<an<6,求出f(an),在求和即可;
,可知2<an<6,求出f(an),在求和即可;
(Ⅲ)由f(b1)+f(b2)+f(b3)=4,且b1=1,得f(q)+f(q2)=3,分类讨论即可求得结果.
解答:解: (I)当x∈[0,
(I)当x∈[0, )时,f(x)=0,
)时,f(x)=0,
当x∈[ ,
, )时,f(x)=1,
)时,f(x)=1,
当x∈[ ,
, )时,f(x)=2,
)时,f(x)=2,
当x∈[ ,
, )时,f(x)=3,
)时,f(x)=3,
当x∈[ ,4]时,f(x)=4,
,4]时,f(x)=4,
∴图象如图所示,
(II)由于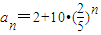 ,所以
,所以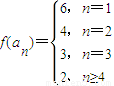 ,
,
因此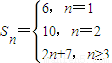 ;
;
(III)由f(b1)+f(b2)+f(b3)=4,且b1=1,得f(q)+f(q2)=3,
当0<q≤1时,则q2≤q≤1,
所以f(q2)≤f(q)≤f(1)=1,
则f(q)+f(q2)≤2<3,不合题意;
当q>1时,则q2>q>1,
所以f(q2)≥f(q)≥f(1)=1.
又f(q)+f(q2)=3,
∴只可能是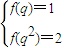 ,即
,即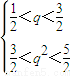 ,
,
解之得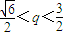 .
.
点评:本题以新定义为载体,考查分段函数的解析式的求法和图象的画法,以及数列求和问题,考查利用知识分析解决问题的能力和运算能力,读懂题意是解题的关键,属难题.
(Ⅱ)根据
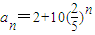 ,可知2<an<6,求出f(an),在求和即可;
,可知2<an<6,求出f(an),在求和即可;(Ⅲ)由f(b1)+f(b2)+f(b3)=4,且b1=1,得f(q)+f(q2)=3,分类讨论即可求得结果.
解答:解:
 (I)当x∈[0,
(I)当x∈[0, )时,f(x)=0,
)时,f(x)=0,当x∈[
 ,
, )时,f(x)=1,
)时,f(x)=1,当x∈[
 ,
, )时,f(x)=2,
)时,f(x)=2,当x∈[
 ,
, )时,f(x)=3,
)时,f(x)=3,当x∈[
 ,4]时,f(x)=4,
,4]时,f(x)=4,∴图象如图所示,
(II)由于
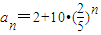 ,所以
,所以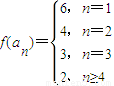 ,
,因此
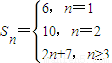 ;
;(III)由f(b1)+f(b2)+f(b3)=4,且b1=1,得f(q)+f(q2)=3,
当0<q≤1时,则q2≤q≤1,
所以f(q2)≤f(q)≤f(1)=1,
则f(q)+f(q2)≤2<3,不合题意;
当q>1时,则q2>q>1,
所以f(q2)≥f(q)≥f(1)=1.
又f(q)+f(q2)=3,
∴只可能是
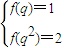 ,即
,即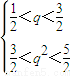 ,
,解之得
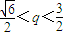 .
.点评:本题以新定义为载体,考查分段函数的解析式的求法和图象的画法,以及数列求和问题,考查利用知识分析解决问题的能力和运算能力,读懂题意是解题的关键,属难题.

练习册系列答案
相关题目