题目内容
(2013•蓟县二模)在△ABC中,A,C为锐角,角A,B,C所对应的边分别为a,b,c,且cos2A=
,sinC=
(Ⅰ)求cos(A+C)的值;
(Ⅱ)若a-c=
-1,求a,b,c的值;
(Ⅲ)求函数y=tan(
+A+C)的最小正周期和定义域.
| 3 |
| 5 |
| ||
| 10 |
(Ⅰ)求cos(A+C)的值;
(Ⅱ)若a-c=
| 2 |
(Ⅲ)求函数y=tan(
| x |
| 2 |
分析:(I)根据二倍角三角函数与同角三角函数的关系,算出cosA、sinA和cosC的值,最后用两角和的余弦公式,即可求出cos(A+C)的值;
(II)由(I)求出的cos(A+C)值,可得A+C=
,从而算出sinB=
,结合正弦定理得出
a=
b=
c,再结合题意a-c=
-1,即可得出三边a,b,c的值;
(III)根据(II)先求出函数的解析式,从而利用最小正周期的公式求出最小正周期,再由利用正弦函数的特点求出函数的定义域即可.
(II)由(I)求出的cos(A+C)值,可得A+C=
| π |
| 4 |
| ||
| 2 |
| 5 |
| 2 |
| 10 |
| 2 |
(III)根据(II)先求出函数的解析式,从而利用最小正周期的公式求出最小正周期,再由利用正弦函数的特点求出函数的定义域即可.
解答:解:(I)∵A,C为锐角,sinC=
sinC=
=
又cos2A=1-2sin2A=
,
∴sinA=
,cosA=
=
∴cos(A+C)=cosAcosC-sinAsinC=
(II)∵cos(A+C)=
0<A+C<π
∴A+C=
∴B=
sinB=
由正弦定理得
=
=
∴
a=
b=
c
即a=
c,b=
c
∵a-c=
-1,∴
c-c=
-1
∵a-c=
-1,∴
c-c=
-1,
∴c=1 a=
,b=
(III)由(II)知A+C=
则y=tan(
+
)
∴函数y=tan(
+
)的最小正周期为2π,
+
≠kπ+
(k∈Z)
解得:x≠2kπ+
(k∈Z)
∴函数y=tan(
+
)的定义域为{x|x≠2kπ+
(k∈Z)}.
| ||
| 10 |
sinC=
| 1-sin2C |
3
| ||
| 10 |
又cos2A=1-2sin2A=
| 3 |
| 5 |
∴sinA=
| ||
| 5 |
| 1-sin2A |
2
| ||
| 5 |
∴cos(A+C)=cosAcosC-sinAsinC=
| ||
| 2 |
(II)∵cos(A+C)=
| ||
| 2 |
0<A+C<π
∴A+C=
| π |
| 4 |
∴B=
| 3π |
| 4 |
| ||
| 2 |
由正弦定理得
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴
| 5 |
| 2 |
| 10 |
即a=
| 2 |
| 5 |
∵a-c=
| 2 |
| 2 |
| 2 |
∵a-c=
| 2 |
| 2 |
| 2 |
∴c=1 a=
| 2 |
| 5 |
(III)由(II)知A+C=
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
∴函数y=tan(
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得:x≠2kπ+
| π |
| 2 |
∴函数y=tan(
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
点评:此题考查了正弦定理、二倍角公式以及三角函数的周期、定义域的求法,有一定的难度,解题过程中要认真、仔细.

练习册系列答案
相关题目
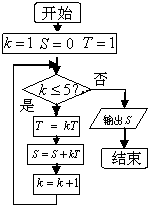 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )