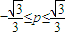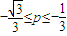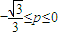题目内容
设非空集合M={x|p≤x≤q}满足:当n∈M时,有n2∈M.现q=
,则p的范围是( )
| 1 |
| 3 |
A、0≤p≤
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
分析:由已知中非空集合M={x|p≤x≤q}满足:当n∈M时,有n2∈M,由q=
<1,我们可以分p>0和p≤0两种情况,讨论p的取值范围,最后综合讨论结果即可得到满足条件的p的范围.
| 1 |
| 3 |
解答:解:集合M={x|p≤x≤q},q=
,
故当p>0时,若n=p,p2<p∉M,
当p≤0时,若n=p,且p2∈M,则p2≤
,即p≥
故-
≤p≤0
故选D
| 1 |
| 3 |
故当p>0时,若n=p,p2<p∉M,
当p≤0时,若n=p,且p2∈M,则p2≤
| 1 |
| 3 |
| ||
| 3 |
故-
| ||
| 3 |
故选D
点评:本题考查的知识点是集合关系中的参数取值问题,其中对p值的分类讨论非常必要,而确定分类的标准,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则p的范围是
,则p的范围是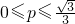
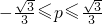
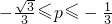
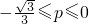
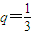 ,则p的范围是( )
,则p的范围是( )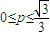
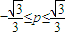

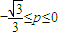
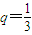 ,则p的范围是( )
,则p的范围是( )