题目内容
【题目】已知函数![]() ,其中e是自然对数的底数.
,其中e是自然对数的底数.
(1)若![]() ,证明:
,证明:![]() ;
;
(2)若![]() 时,都有
时,都有![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)证明见解析(2)![]()
【解析】
(1)当![]() 时,
时,![]() ,利用导数求出函数
,利用导数求出函数![]() 的单调区间并求出最小值,即可证明
的单调区间并求出最小值,即可证明![]() ;
;
(2)令![]() ,由
,由![]() 时,都有
时,都有![]() ,可得
,可得![]() 在
在![]() 上恒成立,利用导数判断
上恒成立,利用导数判断![]() 在
在![]() 的单调性,分别讨论
的单调性,分别讨论![]() 和
和![]() 两种情况,即可得到
两种情况,即可得到![]() 的取值范围.
的取值范围.
(1)由题意,当![]() 时,
时,![]() ,
,
所以![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以![]() 在
在![]() 时取得极小值,也是最小值.
时取得极小值,也是最小值.
所以![]() .
.
(2)令![]() ,
,![]() ,
,
由![]() 时,都有
时,都有![]() ,所以
,所以![]() 在
在![]() 上恒成立.
上恒成立.
由![]() ,令
,令![]() ,
,
则![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
①当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,满足题意.
,满足题意.
②当![]() 时,因为
时,因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
存在![]() ,使得当
,使得当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ,这与
,这与![]() 在
在![]() 上恒成立矛盾.
上恒成立矛盾.
综上所述,![]() ,即实数a的取值范围
,即实数a的取值范围![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】某外卖平台为提高外卖配送效率,针对外卖配送业务提出了两种新的配送方案,为比较两种配送方案的效率,共选取50名外卖骑手,并将他们随机分成两组,每组25人,第一组骑手用甲配送方案,第二组骑手用乙配送方案.根据骑手在相同时间内完成配送订单的数量(单位:单)绘制了如下茎叶图:
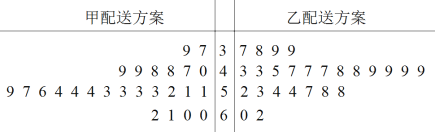
(1)根据茎叶图,求各组内25位骑手完成订单数的中位数,已知用甲配送方案的25位骑手完成订单数的平均数为52,结合中位数与平均数判断哪种配送方案的效率更高,并说明理由;
(2)设所有50名骑手在相同时间内完成订单数的平均数![]() ,将完成订单数超过
,将完成订单数超过![]() 记为“优秀”,不超过
记为“优秀”,不超过![]() 记为“一般”,然后将骑手的对应人数填入下面列联表;
记为“一般”,然后将骑手的对应人数填入下面列联表;
优秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根据(2)中的列联表,判断能否有![]() 的把握认为两种配送方案的效率有差异.
的把握认为两种配送方案的效率有差异.
附: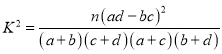 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中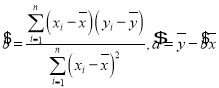 )
)