题目内容
如图:设一正方形ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,使A、B、C、D四点重合,记为A点.恰好能做成一个正四棱锥(粘贴损耗不计),图中AH⊥PQ,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.

(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.

分析:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,由此先计算出此正四棱锥的棱长,再利用正棱锥的性质计算其体积即可;
(II)先利用等腰三角形APQ的底角为x的特点,将侧棱长和底边长分别表示为x的函数,再利用棱锥的体积计算公式将棱锥体积表示为关于x的函数,最后可利用均值定理求函数的值域
(II)先利用等腰三角形APQ的底角为x的特点,将侧棱长和底边长分别表示为x的函数,再利用棱锥的体积计算公式将棱锥体积表示为关于x的函数,最后可利用均值定理求函数的值域
解答:解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,
∵正方形ABCD边长为2分米,∴AH=
a=
=
,解得a=
=
-
∴正四棱锥的棱长a=
-
∴PO=
a,AO=
=
a,
∴V=
×a2×AO=
a3=
×(
-
)3=4
-

(II)∵AH=
PQ×tanx=
=
=
-
PQ
∴PQ=
,AH=
∴S=4×
×PQ×AH
=2×PQ×AH
=2×
×
=
x∈[
,
)
∵S=
=
=
≤
=2 (当且仅当tanx=1即x=
时取等号)
而tanx>0,故s>0
∵S等于2时三角形APQ是等腰直角三角形,顶角PAQ等于90°,阴影部分不存在,折叠后A与O重合,构不成棱锥,∴S的范围为(0,2).
∵正方形ABCD边长为2分米,∴AH=
| ||
| 2 |
| AC-a |
| 2 |
2
| ||
| 2 |
2
| ||
1+
|
| 6 |
| 2 |
∴正四棱锥的棱长a=
| 6 |
| 2 |
∴PO=
| ||
| 2 |
| AP2-PO2 |
| ||
| 2 |
∴V=
| 1 |
| 3 |
| ||
| 6 |
| ||
| 6 |
| 6 |
| 2 |
| 3 |
| 20 |
| 3 |

(II)∵AH=
| 1 |
| 2 |
| AC-PQ |
| 2 |
2
| ||
| 2 |
| 2 |
| 1 |
| 2 |
∴PQ=
2
| ||
| 1+tanx |
| ||
| 1+tanx |
∴S=4×
| 1 |
| 2 |
=2×PQ×AH
=2×
2
| ||
| 1+tanx |
| ||
| 1+tanx |
=
| 8tanx |
| (1+tanx) 2 |
| π |
| 4 |
| π |
| 2 |
∵S=
| 8tanx |
| (1+tanx) 2 |
| 8tanx |
| 1+tan2x+2tanx |
| 8 | ||
|
| 8 |
| 2+2 |
| π |
| 4 |
而tanx>0,故s>0
∵S等于2时三角形APQ是等腰直角三角形,顶角PAQ等于90°,阴影部分不存在,折叠后A与O重合,构不成棱锥,∴S的范围为(0,2).
点评:本题主要考查了正四棱锥的几何性质,正四棱锥中的棱长、高、体积的计算,建立函数模型并求其最值的方法,有一定的难度

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
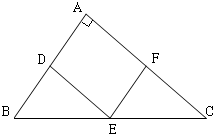 如图,Rt△ABC内有一内接正方形ADEF,它的两条边AD,AF分别在直角边AB,AC上.设BC=a,∠ABC=θ.
如图,Rt△ABC内有一内接正方形ADEF,它的两条边AD,AF分别在直角边AB,AC上.设BC=a,∠ABC=θ.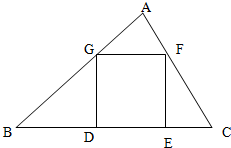 在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,如图所示.
在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,如图所示. 如图,BC是东西方向长为2km的公路,现考虑在点C的正北 方向的点A处建一仓库,设AC=xkm,并在AB上选择一点F,在△ABC内建造边长为ykm的正方形中转站EFGH,其中边HG在公路BC上,且AE=AC.
如图,BC是东西方向长为2km的公路,现考虑在点C的正北 方向的点A处建一仓库,设AC=xkm,并在AB上选择一点F,在△ABC内建造边长为ykm的正方形中转站EFGH,其中边HG在公路BC上,且AE=AC. (2009•滨州一模)如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且
(2009•滨州一模)如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且 (2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ASCD.设AB=2.
(2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ASCD.设AB=2.