Question

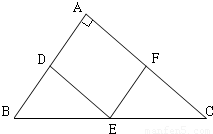
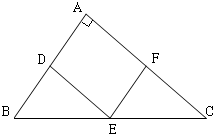如图，Rt△ABC内有一内接正方形ADEF，它的两条边AD，AF分别在直角边AB，AC上．设BC=a，∠ABC=θ．
（1）求△ABC的面积P和正方形的面积Q；
（2）当θ变化时，求

P

Q

的最小值．

Answer 1

分析：（1）设出正方形的变成为x，由BC=a，∠ABC=θ，在直角三角形ABC中，利用锐角三角函数定义表示出直角边AB和AC，即可求出直角三角形ABC的面积；在直角三角形BDE中，由DE=x，∠ABC=θ，根据锐角三角形函数定义表示出BD，根据BD+AD=AB列出关于x的方程，求出方程的解得到x的值，分子分母同时乘以tanθ，利用同角三角函数间的基本关系化简后，得到正方形的边长，平方即可得到正方形的面积；
（2）将第一问表示出的P和Q代入

P

Q

，约分化简后，根据θ的范围，得到tanθ的范围，设tanθ=t，进而得到t的范围，设化简后的式子为g（t），由t大于0，利用基本不等式求出t+

1

t

的最小值及取最小值时t的值，即可得到g（t）的最小值，即为所求式子的最小值．

解答：解：（1）设正方边的边长为x，
则有AD=DE=x，BD=xcotθ，AB=acosθ，AC=asinθ，
∴xcotθ+x=acosθ，x=

acosθ

1+cotθ

=

acosθtanθ

(1+cotθ)tanθ

=

asinθ

tanθ+1

，
则P=

1

2

AB•AC=

1

2

a2cosθsinθ，（2分）Q=

a2sin2θ

(tanθ+1)2

；（6分）

（2）

P

Q

=

1 2 a2cosθsinθ

a2sin2θ (tanθ+1)2

=

(tanθ+1)2

2tanθ

=

1

2

(tanθ+

1

tanθ

)+1，（9分）
设t=tanθ，∵0＜θ＜

π

2

，∴t∈（0，+∞），
令g(t)=

1

2

(t+

1

t

)+1(t＞0)，
∵t+

1

t

≥2，当且仅当t=

1

t

，即t=1时取等号，
∴当t=1，即θ=

π

4

时，g（t）有最小值，且最小值为2，（11分）
则

P

Q

最小值为2．（13分）

点评：此题考查了三角函数的定义，同角三角函数间的基本关系，以及基本不等式，第一问的思路是：设出正方形的边长，利用锐角三角形函数定义，建立三角形的边角关系，列出关于x的方程，求出正方形的边长，进而表示出P和Q；第二问思路为：把表示出的P和Q代入所求式子中，变形后，利用基本不等式即可求出所求式子的最小值．