题目内容
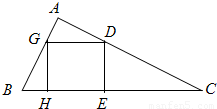
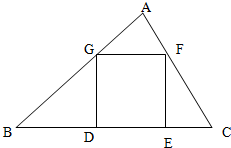在Rt△ABC内有一内接正方形，它的一条边在斜边BC上，如图所示．（1）设AB=a，∠ABC=θ，求Rt△ABC的面积P和正方形的面积Q
（2）当θ变化时，求
| P | Q |
分析：（1）设正方形边长为x，求出BC=
，AC=atanθ，x，即可求出三角形ABC的面积P，正方形的面积Q．
（2）利用（1）推出
的表达式，利用函数的单调性，求出比值的最小值．
| a |
| cosθ |
（2）利用（1）推出
| P |
| Q |
解答：解：（1）设正方形边长为x
AB=a，∠ABC=θ
BC=
，AC=atanθ
BD=xcotθ，EC=xtanθ
BC=
=BD+DE+EC=x+xcotθ+xtanθ
x=
=
三角形ABC的面积P=
AB×AC=
a2tanθ
正方形的面积 Q=x2=(
)2．
（2）
=
×
=
+
sinθcosθ+1
∵sinθ＞0，cosθ＞0
令：t=sin2θ
∵0＜θ＜
∴t∈（0，1]∴
=1+
+
，函数在（0，1]递减
∴ymin=
（当且仅当t=1即θ=
时成立）
∴当θ=
时，
的最小值为
．
AB=a，∠ABC=θ
BC=
| a |
| cosθ |
BD=xcotθ，EC=xtanθ
BC=
| a |
| cosθ |
x=
| a |
| (1+cotθ+tanθ)cosθ |
| asinθ |
| sinθcosθ+1 |
三角形ABC的面积P=
| 1 |
| 2 |
| 1 |
| 2 |
正方形的面积 Q=x2=(
| asinθ |
| sinθcosθ+1 |
（2）
| P |
| Q |
| 1 |
| 2 |
| a2tanθ | ||
(
|
=
| 1 |
| 2sinθcosθ |
| 1 |
| 2 |
∵sinθ＞0，cosθ＞0
令：t=sin2θ
∵0＜θ＜
| π |
| 2 |
∴t∈（0，1]∴
| P |
| Q |
| 1 |
| t |
| t |
| 4 |
∴ymin=
| 9 |
| 4 |
| π |
| 4 |
∴当θ=
| π |
| 4 |
| P |
| Q |
| 9 |
| 4 |
点评：本题考查三角函数的基本关系式，函数单调性的应用，考查计算能力．
练习册系列答案
相关题目
如图所示，在Rt△ABC内有一内接正方形，它的一条边在斜边BC上，设AB=a，∠ABC=θ
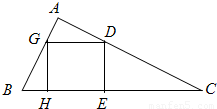
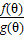的最小值．
的最小值．