题目内容
 如图,BC是东西方向长为2km的公路,现考虑在点C的正北 方向的点A处建一仓库,设AC=xkm,并在AB上选择一点F,在△ABC内建造边长为ykm的正方形中转站EFGH,其中边HG在公路BC上,且AE=AC.
如图,BC是东西方向长为2km的公路,现考虑在点C的正北 方向的点A处建一仓库,设AC=xkm,并在AB上选择一点F,在△ABC内建造边长为ykm的正方形中转站EFGH,其中边HG在公路BC上,且AE=AC.(1)求y关于x的函数解析式;
(2)求正方形中转站EFGH面积的最大值及此时x的值.
分析:(1)延长FE,交AC于D,显然DF∥BC,则Rt△ADF∽Rt△ACB,利用AE=AC=x,求得DE,于是可得方程,然后解方程即可,
(2)由第(1)得y关于x的函数解析式,变形后利用基本不等式得当x=
时,即可求出正方形中转站EFGH面积的最大值的最大值.
(2)由第(1)得y关于x的函数解析式,变形后利用基本不等式得当x=
| 2 |
| x |
解答: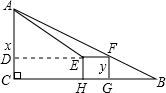 解:(1)如图,延长FE,交AC于D,
解:(1)如图,延长FE,交AC于D,
∵DF∥BC,
∴Rt△ADF∽Rt△ACB,
∴AE=AC=X,知:DE=
=
,
∴
=
⇒2x-2y-xy=x
,
两边平方,并整理得(x2+2x+2)y2-(x3+2x2+4x)y+2x2=0,
解得:y=
(另一解y=x舍去).
答:y关于x的函数解析式为y=
.
(2)由第(1)题得y=
=
≤
当x=
,即x=
时,y有最大值=
=
-1,
∴当x=
时,正方形中转站EFGH面积的最大值最大值为(
-1)2=3-2
.
 解:(1)如图,延长FE,交AC于D,
解:(1)如图,延长FE,交AC于D,∵DF∥BC,
∴Rt△ADF∽Rt△ACB,
∴AE=AC=X,知:DE=
| x2-(x-y)2 |
| 2xy-y2 |
∴
| x-y |
| x |
| ||
| 2 |
| 2xy-y2 |
两边平方,并整理得(x2+2x+2)y2-(x3+2x2+4x)y+2x2=0,
解得:y=
| 2x |
| x2+2x+2 |
答:y关于x的函数解析式为y=
| 2x |
| x2+2x+2 |
(2)由第(1)题得y=
| 2x |
| x2+2x+2 |
| 2 | ||
x+
|
| 2 | ||
2
|
当x=
| 2 |
| x |
| 2 |
| 2 | ||
2
|
| 2 |
∴当x=
| 2 |
| 2 |
| 2 |
点评:此题涉及到相似三角形的判定与性质,直角三角形的性质,正方形的性质等多个知识点,有一定的拔高难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目