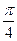题目内容
设f(x)=
|x2-a2|dx.
(1)当0≤a≤1与a>1时,分别求f(a);
(2)当a≥0时,求f(a)的最小值.
| ∫ | 10 |
(1)当0≤a≤1与a>1时,分别求f(a);
(2)当a≥0时,求f(a)的最小值.
(1)0≤a≤1时,
f(a)=
|x2-a2|dx
=
(a2-x2)dx+
(x2-a2)dx
=(a2x-
x3)
+(
-a2x)
=a3-
a3-0+0+
-a2-
+a3
=
a3-a2+
.
当a>1时,
f(a)=
(a2-x2)dx
=(a2x-
x3)
=a2-
.
∴f(a)=
(2)当a>1时,由于a2-
在[1,+∞)上是增函数,故f(a)在[1,+∞)上的最小值是f(1)=1-
=
.
当a∈[0,1]时,f′(a)=4a2-2a=2a(2a-1),
由f′(a)>0知:a>
或a<0,
故在[0,
]上递减,在[
,1]上递增.
因此在[0,1]上,f(a)的最小值为f(
)=
.
综上可知,f(x)在[0,+∞)上的最小值为
.
f(a)=
| ∫ | 10 |
=
| ∫ | a0 |
| ∫ | 1a |
=(a2x-
| 1 |
| 3 |
| . |
|
| x3 |
| 3 |
| . |
|
=a3-
| 1 |
| 3 |
| 1 |
| 3 |
| a3 |
| 3 |
=
| 4 |
| 3 |
| 1 |
| 3 |
当a>1时,
f(a)=
| ∫ | 10 |
=(a2x-
| 1 |
| 3 |
| . |
|
=a2-
| 1 |
| 3 |
∴f(a)=
|
(2)当a>1时,由于a2-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
当a∈[0,1]时,f′(a)=4a2-2a=2a(2a-1),
由f′(a)>0知:a>
| 1 |
| 2 |
故在[0,
| 1 |
| 2 |
| 1 |
| 2 |
因此在[0,1]上,f(a)的最小值为f(
| 1 |
| 2 |
| 1 |
| 4 |
综上可知,f(x)在[0,+∞)上的最小值为
| 1 |
| 4 |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
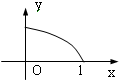
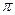 ,宽为2的矩形
,宽为2的矩形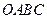 内,曲线
内,曲线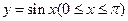 与
与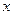 轴围成如图所示的阴影部分,向矩形
轴围成如图所示的阴影部分,向矩形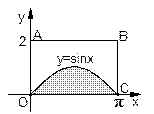
 B.
B.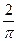 C.
C. 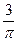 D.
D.