题目内容

（1）已知-1≤x≤2，且x≠0，求lg|x|+lg|7-x|的最大值．
（2）已知x∈R，求函数y=3（4^x+4^-x）-10（2^x+2^-x）的最小值．
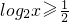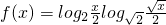（3）已知2^x≤256且 $数学公式$ ，求函数 $数学公式$ 的最大值和最小值．

解：（1）lg|x|+lg|7-x|=lg|7x-x²|．∵-1≤x≤2∴7x-x²∈[-8，10]，|7x-x²|∈[0，10]∴最大值为1（此时x=2）
（2）令t=（2^x+2^-x）（t≥2），则y=3t²-10t-6（t≥2），∴y≥-14（此时x=1）
（3）由已知， $\text{[math]}$ ，f（x）=（log₂x-1）（log₂x-2）=log₂²x-3log₂x+2，令t=log₂x
则y=t²-3t+2，函数f（x）的最小值为 $\text{[math]}$ （此时x=8），最大值为2（此时 $\text{[math]}$ ）
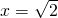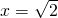分析：（1）将lg|x|+lg|7-x|化为lg|7x-x²|，通过求7x-x^{2_{的取值范围解决．
（2）令}}t=（2^x+2^-x）进行换元．转化为二次函数解决．
（3）根据对数的运算法则，，f（x）=（log₂x-1）（log₂x-2）=log₂²x-3log₂x+2，令t=log₂x，转化为二次函数解决．
点评：本题考查对数的运算，二次函数性质、换元法，考查分析解决问题、计算能力．

练习册系列答案

Happy寒假作业快乐寒假系列答案

金象教育U计划学期系统复习寒假作业系列答案

八斗才火线计划寒假西安交通大学出版社系列答案

伴你成长橙色寒假系列答案

帮你学寒假作业系列答案

备战中考寒假系列答案

创新大课堂系列丛书寒假作业系列答案

创新自主学习寒假新天地系列答案

创优教学寒假作业年度总复习系列答案

导学练寒假作业云南教育出版社系列答案

相关题目

（1）已知矩阵A=

3	3
2	4

，
（Ⅰ）求矩阵A的特征值和对应的特征向量；
（Ⅱ）求向量α，使得A²α=β．
（2）在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点A、B的极坐标分别为（1，0）、(1，

)，曲线C的参数方程为

(α为参数，r＞0）
（Ⅰ）求直线AB的直角坐标方程；
（Ⅱ）若直线AB和曲线C只有一个交点，求r的值．
（3）设不等式|x-2|＞1的解集与关于x的不等式x²-ax+b＞0的解集相同．
（Ⅰ）求a，b的值；
（Ⅱ）求函数f(x)=a

的最大值，以及取得最大值时x的值．

给出下列四个命题：
①已知f(x)+2f(

)=3x，则函数g（x）=f（2^x）在（0，1）上有唯一零点；
②对于函数f(x)=x

的定义域中任意的x₁、x₂（x₁≠x₂）必有f(

；
③已知f（x）=|2^-x+1-1|，a＜b，f（a）＜f（b），则必有0＜f（b）＜1；
④已知f（x）、g（x）是定义在R上的两个函数，对任意x、y∈R满足关系式f（x+y）+f（x-y）=2f（x）•g（y），且f（0）=0，但x≠0时f（x）•g（x）≠0．则函数f（x）、g（x）都是奇函数．
其中正确命题的序号是

对于函数f（x），g（x），h（x），如果存在实数a，b，使得h（x）=af（x）+bg（x），那么称h（x）为f（x），g（x）的线性生成函数．
（1）给出如下两组函数，试判断h（x）是否分别为f（x），g（x）的线性生成函数，并说明理由．
第一组：f(x)=sinx，g(x)=cosx，h(x)=sin(x+

)；
第二组：f（x）=x²-x，g（x）=x²+x+1，h（x）=x²-x+1．
（2）已知f（x）=log₂x，g（x）=log_0.5x的线性生成函数为h（x），其中a=2，b=1．若不等式3h²（x）+2h（x）+t＜0在x∈[2，4]上有解，求实数t的取值范围；
（3）已知f(x)=x，g(x)=

，x∈[1，10]的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．

选修4-5不等式选讲
（1）已知x，y，z∈R，且x²+y²+z²=1，求2x+3y+4z的最小值；
（2）解关于x的不等式：|2x+1|+|x+2|＞5．

(1)已知函数f(x)=x²,g(x)为一次函数，且为增函数，若f［g(x)］=4x²-20x+15,求g(x)的解析式;

(2)已知af(x)+bf()=cx(a、b、c∈R,ab≠0,a²≠b²),求f(x);

(3)f(x)是R上的奇函数，且x∈(-∞,0)时，f(x)=x²+2x,求f(x);

(4)某工厂生产一种机器的固定成本为5 000元，且每生产100部，需要增加投入2 500元，对销售市场进行调查后得知，市场对此产品的需求量为每年500部，已知销售收入的函数为H(x)=500x-x²,其中x是产品售出的数量，且0≤x≤500.若x为年产量，y表示利润，求y=f(x)的解析式.