题目内容
(1)已知函数f(x)=x2,g(x)为一次函数,且为增函数,若f[g(x)]=4x2-20x+15,求g(x)的解析式;(2)已知af(x)+bf(![]() )=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
(3)f(x)是R上的奇函数,且x∈(-∞,0)时,f(x)=x2+2x,求f(x);
(4)某工厂生产一种机器的固定成本为5 000元,且每生产100部,需要增加投入2 500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入的函数为H(x)=500x-![]() x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
思路分析:已知函数的模型(如一次函数、反比例函数、二次函数等)一般设出函数解析式,由题设确定系数,即待定系数法,如(1);求抽象函数解析式,可以以变量换变量,然后解方程组求解析式,如(2),也可根据函数奇偶性确定解析式,如(3);实际应用问题的函数解析式则要符合实际意义.
解:(1)设g(x)=ax+b(a>0),a2x2+2abx+b2=4x2-20x+25(a>0).解得
∴g(x)=2x-5.
(2)由题设af(x)+bf(![]() )=cx,用x代换上式中的
)=cx,用x代换上式中的![]() ,则af(
,则af(![]() )+bf(x)=
)+bf(x)=![]() ,列方程组
,列方程组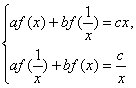 解得f(x)=
解得f(x)=![]() (ax-
(ax-![]() ).
).
(3)由于f(x)的定义域是R,且f(x)是奇函数,可得f(0)=0.
当x>0时,-x<0,则f(-x)=(-x)2-2x=x2-2x.
∴-f(x)=x2-2x,即f(x)=-x2+2x(x>0).
∴f(x)=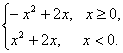
(4)由题意知,当0≤x≤500时,产品全部售出;当x>500时,只能售出500部,故利润函数
y=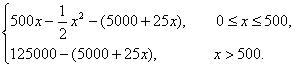
=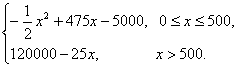

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是
若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是