题目内容
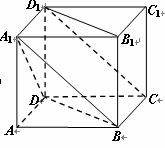
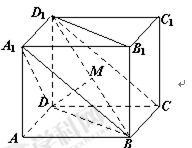
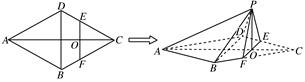
如右图,在底面为平行四边形的四棱柱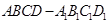 中,
中,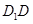
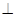 底面
底面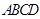 ,
,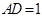 ,
,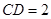 ,
,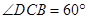 .
.
(1)求证:平面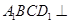 平面
平面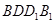 ;
;
(2)若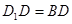 ,求四棱锥
,求四棱锥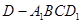 的体积.
的体积.
(1)详见解析(2)1
解析试题分析:(1)由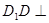 平面
平面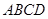 ,可证
,可证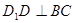 .
.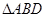 中,勾股定理可得
中,勾股定理可得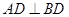 ,由线面垂直的判定定理可证
,由线面垂直的判定定理可证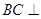 ⊥平面
⊥平面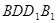 ,再由平面与平面垂直的判定定理可证平面
,再由平面与平面垂直的判定定理可证平面 ;
;
(2)利用(1)中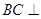 ⊥平面
⊥平面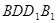 ,取
,取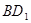 的中点
的中点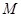 ,根据已知得
,根据已知得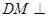 面
面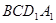 ,四棱锥
,四棱锥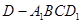 的体积为
的体积为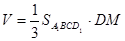 =
=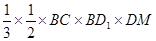 .
.
试题解析:
解:(1)证明:在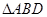 中,由余弦定理得:
中,由余弦定理得: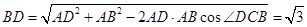 ,
,
所以 ,所以
,所以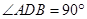 ,即
,即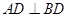 ,
,
又四边形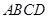 为平行四边形,所以
为平行四边形,所以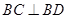 ,
,
又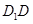
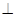 底面
底面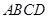 ,
,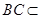 底面
底面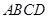 ,所以
,所以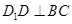 ,
,
又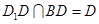 ,所以
,所以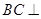 平面
平面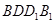 ,
,
又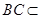 平面
平面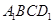 ,所以平面
,所以平面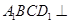 平面
平面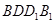 . 6分
. 6分
(2)连结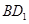 ,
,
∵ ,
,
∴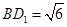
∵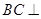 平面
平面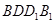 ,
,
所以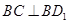 ,
,
所以四边形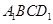 的
的
面积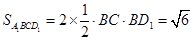 , 8分
, 8分
取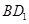 的中点
的中点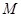 ,连结
,连结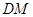 ,则
,则 ,
,
且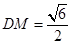 ,又平面
,又平面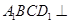 平面
平面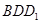 ,平面
,平面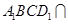 平面
平面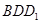
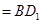 ,
,
所以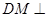 平面
平面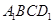 ,所以四棱锥
,所以四棱锥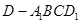 的体积:
的体积: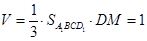 . 12分
. 12分
考点:1.面面垂直的判定定理;2.椎体的体积.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
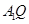 和
和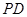 所成的角为
所成的角为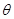 ,求
,求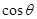 的值.
的值.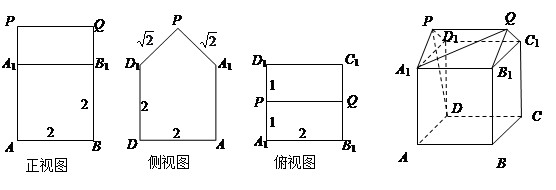
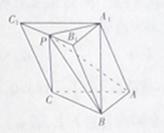
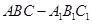 中,侧棱
中,侧棱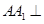 平面
平面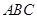 ,
,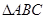 为等腰直角三角形,
为等腰直角三角形,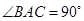 ,且
,且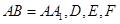 分别是
分别是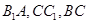 的中点.
的中点.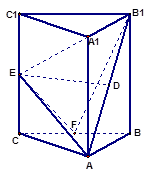
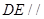 平面
平面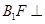 平面
平面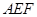 ;
;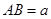 ,求三棱锥
,求三棱锥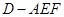 的体积.
的体积. 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?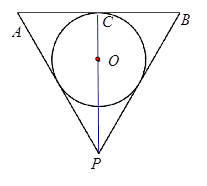
 ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.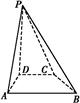
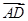 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.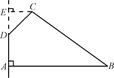
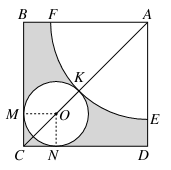
 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.