题目内容
已知在数列{an}中,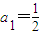 ,Sn是其前n项和,且Sn=n2an-n(n-1).
,Sn是其前n项和,且Sn=n2an-n(n-1).(1)证明:数列
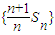 是等差数列;
是等差数列;(2)令bn=(n+1)(1-an),记数列{bn}的前n项和为Tn.
①求证:当n≥2时,
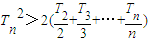 ;
;②)求证:当n≥2时,
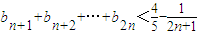 .
.
【答案】分析:(1)由题设知Sn=n2(Sn-Sn-1)-n(n-1),(n2-1)Sn-n2S=n(n-1),两边同除以n(n-1),得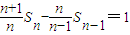 ,由此能够证明数列
,由此能够证明数列 是等差数列;
是等差数列;
(2)由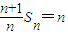 ,
,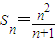 代入Sn=n2an-n(n-1),得
代入Sn=n2an-n(n-1),得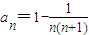 ,故
,故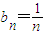 ,
,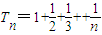 .
.
①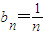 ,
,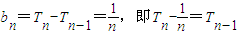 ,平方
,平方 ,
,
再由叠加法能够得到当n≥2时,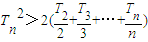 ;
;
②当n=2时,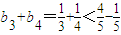 即n=2时命题成立,由数学归纳法能够证明对于任意n≥2,
即n=2时命题成立,由数学归纳法能够证明对于任意n≥2,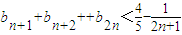 .
.
解答:解:(1)由条件可得Sn=n2(Sn-Sn-1)-n(n-1),(n2-1)Sn-n2S=n(n-1)
两边同除以n(n-1),得: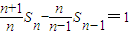
所以:数列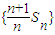 成等差数列,且首项和公差均为(14分)
成等差数列,且首项和公差均为(14分)
(2)由(1)可得: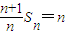 ,
,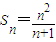 ,代入Sn=n2an-n(n-1)可得
,代入Sn=n2an-n(n-1)可得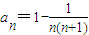 ,所以
,所以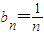 ,
,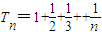 .(6分)
.(6分)
①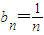 当n≥2时,
当n≥2时,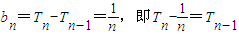
平方则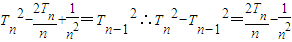
叠加得 ∴
∴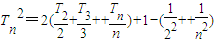
又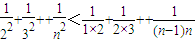
=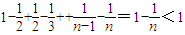 ∴
∴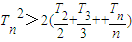 (9分)
(9分)
②当n=2时,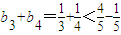 即n=2时命题成立
即n=2时命题成立
假设n=k(k≥2)时命题成立,即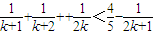
当n=k+1时,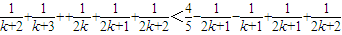
=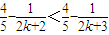 即n=k+1时命题也成立
即n=k+1时命题也成立
综上,对于任意n≥2,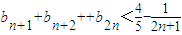 (14分)
(14分)
点评:本题考查数列知识的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.
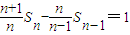 ,由此能够证明数列
,由此能够证明数列 是等差数列;
是等差数列;(2)由
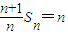 ,
,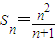 代入Sn=n2an-n(n-1),得
代入Sn=n2an-n(n-1),得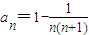 ,故
,故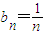 ,
,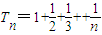 .
.①
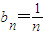 ,
,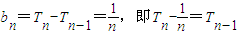 ,平方
,平方 ,
,再由叠加法能够得到当n≥2时,
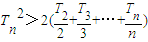 ;
;②当n=2时,
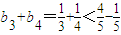 即n=2时命题成立,由数学归纳法能够证明对于任意n≥2,
即n=2时命题成立,由数学归纳法能够证明对于任意n≥2,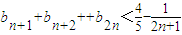 .
.解答:解:(1)由条件可得Sn=n2(Sn-Sn-1)-n(n-1),(n2-1)Sn-n2S=n(n-1)
两边同除以n(n-1),得:
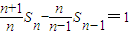
所以:数列
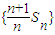 成等差数列,且首项和公差均为(14分)
成等差数列,且首项和公差均为(14分)(2)由(1)可得:
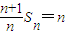 ,
,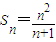 ,代入Sn=n2an-n(n-1)可得
,代入Sn=n2an-n(n-1)可得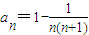 ,所以
,所以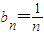 ,
,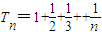 .(6分)
.(6分)①
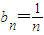 当n≥2时,
当n≥2时,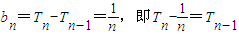
平方则
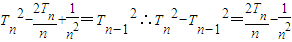
叠加得
 ∴
∴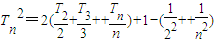
又
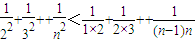
=
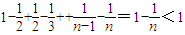 ∴
∴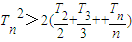 (9分)
(9分)②当n=2时,
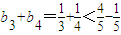 即n=2时命题成立
即n=2时命题成立假设n=k(k≥2)时命题成立,即
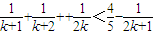
当n=k+1时,
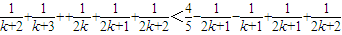
=
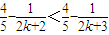 即n=k+1时命题也成立
即n=k+1时命题也成立综上,对于任意n≥2,
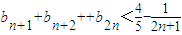 (14分)
(14分)点评:本题考查数列知识的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目