题目内容
1.因式分解:(1)12x2-5x-2
(2)5x2+6xy-8y2.
分析 可以用公式法求出对应方程的实数根,再把二次三项式分解因式.
解答 解:(1)∵12x2-5x-2=0,
△=25-4×12×(-2)=121>0,
∴方程12x2-5x-2=0的两个实数根为x1=$\frac{2}{3}$,x2=-$\frac{1}{4}$;
∴12x2-5x-2=(3x-2)(4x+1);
(2)5x2+6xy-8y2=(5x-4y)(x+2y)
点评 本题考查了二次三项式的因式分解的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知回归直线方程中斜率的估计值为1.23,样本点的中心(5,6.2),则回归直线方程为( )
| A. | y=1.23x-0.05 | B. | y=1.23x+0.05 | C. | y=1.23x+6.2 | D. | y=1.23x+5 |
10.某程序框图如图所示,若其输出结果是56,则判断框中应填写的是( )
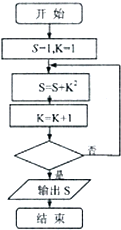

| A. | K<4 | B. | K<5 | C. | K<6 | D. | K<7 |