题目内容
如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO=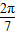 (参考数据:tan
(参考数据:tan
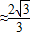 ).今计划建一个生活垃圾中转站P,为方便运输,P准备建在线段AO(不含端点)上.
).今计划建一个生活垃圾中转站P,为方便运输,P准备建在线段AO(不含端点)上.(I)设PO=x(0<x<40),试将P到三个小区距离的最远者S表示为x的函数,并求S的最小值;
(II)设∠PBO=a(0
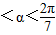 ),试将P到三个小区的距离之和y表示为a的函数,并确定当a取何值时,可使y最小?
),试将P到三个小区的距离之和y表示为a的函数,并确定当a取何值时,可使y最小?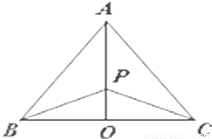
【答案】分析:(1)利用直角三角形的边角关系及其勾股定理、函数的单调性即可得出;
(2)根据条件列出其表达式,利用导数得出其单调性,进而即可得出最小值.
解答:解:(1)在Rt△AOB中,∵AO=40,∠ABO=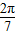 ,∴
,∴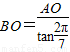 =
=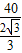 =
=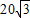 ,
,
∴PA=40-x,PB=PC=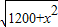 ,
,
①若PA≥PB,即40-x≥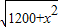 ,即0<x≤5时,S=40-x;
,即0<x≤5时,S=40-x;
②若PA<PB,即40-x<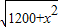 ,即5<x<40时,S=
,即5<x<40时,S=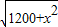 .
.
从而S=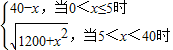 .
.
当0<x≤5时,S=40-x单调递减,∴Smin=35;
当5<x<40时,S=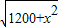 ,是增函数,∴S>S(5)=35.
,是增函数,∴S>S(5)=35.
综上可知:当x=5时,S取得最小值为35.
(2)在Rt△BOP中,BP=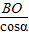 =
=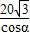 ,PO=BOtanα=
,PO=BOtanα=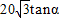 ,
,
∴y=2BP+(AO-PO)=40+2BP-PO=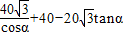 =40+
=40+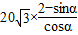
∵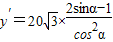 ,令y′=0,即
,令y′=0,即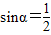 ,从而
,从而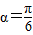 ,
,
当0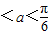 时,y′<0;当
时,y′<0;当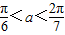 时,y′>0.
时,y′>0.
当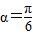 时,可使y最小.
时,可使y最小.
点评:数列掌握勾股定理、利用导数研究函数的单调性是解题的关键.
(2)根据条件列出其表达式,利用导数得出其单调性,进而即可得出最小值.
解答:解:(1)在Rt△AOB中,∵AO=40,∠ABO=
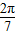 ,∴
,∴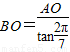 =
=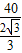 =
=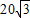 ,
,∴PA=40-x,PB=PC=
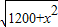 ,
,①若PA≥PB,即40-x≥
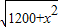 ,即0<x≤5时,S=40-x;
,即0<x≤5时,S=40-x;②若PA<PB,即40-x<
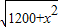 ,即5<x<40时,S=
,即5<x<40时,S=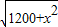 .
.从而S=
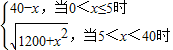 .
.当0<x≤5时,S=40-x单调递减,∴Smin=35;
当5<x<40时,S=
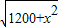 ,是增函数,∴S>S(5)=35.
,是增函数,∴S>S(5)=35.综上可知:当x=5时,S取得最小值为35.
(2)在Rt△BOP中,BP=
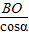 =
=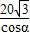 ,PO=BOtanα=
,PO=BOtanα=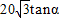 ,
,∴y=2BP+(AO-PO)=40+2BP-PO=
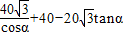 =40+
=40+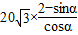
∵
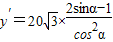 ,令y′=0,即
,令y′=0,即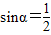 ,从而
,从而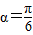 ,
,当0
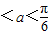 时,y′<0;当
时,y′<0;当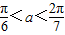 时,y′>0.
时,y′>0.当
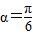 时,可使y最小.
时,可使y最小.点评:数列掌握勾股定理、利用导数研究函数的单调性是解题的关键.

练习册系列答案
相关题目
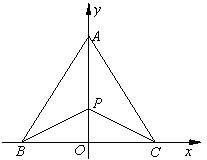 有三个生活小区,分别位于A,B,C三点处,且
有三个生活小区,分别位于A,B,C三点处,且 如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO=
如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO= 有三个生活小区,分别位于
有三个生活小区,分别位于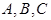 三点处,
三点处,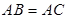 ,
,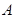 到线段
到线段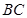 的距离
的距离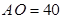 ,
,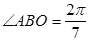 (参考数据:
(参考数据: 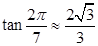 ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站 ,为方便运输,
,为方便运输,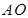 (不含端点)上.
(不含端点)上.
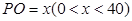 ,试将
,试将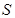 表示为
表示为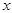 的函数,并求
的函数,并求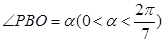 ,试将
,试将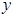 表示为
表示为 的函数,并确定当
的函数,并确定当