题目内容
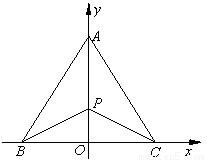
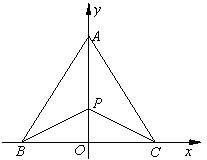 有三个生活小区,分别位于A,B,C三点处,且AB=AC=20
有三个生活小区,分别位于A,B,C三点处,且AB=AC=20| 7 |
| 3 |
| 2 |
| 7 |
(Ⅰ)若希望变电站P到三个小区的距离和最小,点P应位于何处?
(Ⅱ)若希望点P到三个小区的最远距离为最小,点P应位于何处?
分析:(Ⅰ)方法一:∠PBO=α,表示出点P到A,B,C的距离之和为y,利用导数,求出函数的最小值;
方法二:设点P(0,b)(0≤b≤40),P到A,B,C的距离之和为f(b)=40-b+2
(0≤b≤40),再利用导数求出函数的最小值.
(Ⅱ)设点P(0,b)(0≤b≤40),则|PA|=40-b,点P到A,B,C三点的最远距离为g(b)求出
g(b)=
,当0≤b≤5时,g(b)=40-b在[0,5]上是减函数,当5<b≤40时,g(b)=
在(5,40]上是增函数,推出g(b)>g(5)=35,得到当b=5时,g(b)min=35,这时点P在OA上距O点5km.
方法二:设点P(0,b)(0≤b≤40),P到A,B,C的距离之和为f(b)=40-b+2
| b2+1200 |
(Ⅱ)设点P(0,b)(0≤b≤40),则|PA|=40-b,点P到A,B,C三点的最远距离为g(b)求出
g(b)=
|
| b2+1200 |
解答: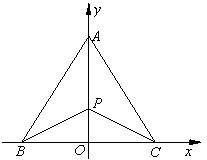 解:在Rt△AOB中,y=k2x,则|OA|=
解:在Rt△AOB中,y=k2x,则|OA|=
=40(1分)
(Ⅰ)方法一:∠PBO=α(0≤α≤
π),
点P到A,B,C的距离之和为y=2×
+40-20
tanα=40+20
×
(5分)y′=20
×
,令y′=0即sinα=
,
又0≤α≤
π,从而α=
当0≤α<
时,y′<0;当
<α≤
时,y'>0.
∴当α=
时,y=40+20
×
取得最小值
此时OP=20
tan
=20
×
=20,
即点P为OA的中点.(8分)
方法二:设点P(0,b)(0≤b≤40),
则P到A,B,C的距离之和为f(b)=40-b+2
(0≤b≤40),
求导得f′(b)=
-1(5分)
由f'(b)=0即2b=
,解得b=20
当0≤b<20时,f′(b)<0;当20<b≤40时,f'(b)>0
∴当b=20时,f(b)取得最小值,此时点P为OA的中点.(8分)
(Ⅱ)设点P(0,b)(0≤b≤40),则|PA|=40-b,|PB|=|PC|=
点P到A,B,C三点的最远距离为g(b)
①若|PA|≥|PB|即40-b≥
?0≤b≤5,则g(b)=40-b;
②若|PA|<|PB|即40-b<
?5<b≤40,则g(b)=
;
∴g(b)=
(11分)
当0≤b≤5时,g(b)=40-b在[0,5]上是减函数,∴g(b)min=g(5)=35
当5<b≤40时,g(b)=
在(5,40]上是增函数,∴g(b)>g(5)=35
∴当b=5时,g(b)min=35,这时点P在OA上距O点5km.(14分)
 解:在Rt△AOB中,y=k2x,则|OA|=
解:在Rt△AOB中,y=k2x,则|OA|=(20
|
(Ⅰ)方法一:∠PBO=α(0≤α≤
| 2 |
| 7 |
点P到A,B,C的距离之和为y=2×
20
| ||
| cosα |
| 3 |
| 3 |
| 2-sinα |
| cosα |
| 3 |
| 2sinα-1 |
| cos2α |
| 1 |
| 2 |
又0≤α≤
| 2 |
| 7 |
| π |
| 6 |
当0≤α<
| π |
| 6 |
| π |
| 6 |
| 2π |
| 7 |
∴当α=
| π |
| 6 |
| 3 |
| 2-sinα |
| cosα |
此时OP=20
| 3 |
| π |
| 6 |
| 3 |
| ||
| 3 |
即点P为OA的中点.(8分)
方法二:设点P(0,b)(0≤b≤40),
则P到A,B,C的距离之和为f(b)=40-b+2
| b2+1200 |
求导得f′(b)=
| 2b | ||
|
由f'(b)=0即2b=
| b2+1200 |
当0≤b<20时,f′(b)<0;当20<b≤40时,f'(b)>0
∴当b=20时,f(b)取得最小值,此时点P为OA的中点.(8分)
(Ⅱ)设点P(0,b)(0≤b≤40),则|PA|=40-b,|PB|=|PC|=
| b2+1200 |
点P到A,B,C三点的最远距离为g(b)
①若|PA|≥|PB|即40-b≥
| b2+1200 |
②若|PA|<|PB|即40-b<
| b2+1200 |
| b2+1200 |
∴g(b)=
|
当0≤b≤5时,g(b)=40-b在[0,5]上是减函数,∴g(b)min=g(5)=35
当5<b≤40时,g(b)=
| b2+1200 |
∴当b=5时,g(b)min=35,这时点P在OA上距O点5km.(14分)
点评:本题考查两点间距离公式的应用,利用导数求闭区间上函数的最值,考查分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
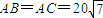 ,
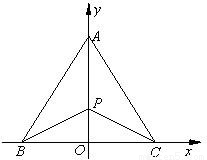
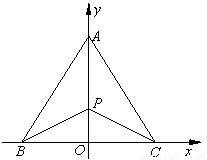
,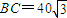 .今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且
.今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且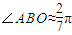 .
.
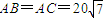 ,
,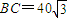 .今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且
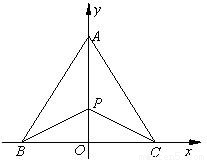
.今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且 .
.
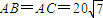 ,
,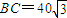 .今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且
.今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且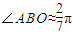 .
.
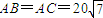 ,
,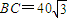 .今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且
.今计划合建一个变电站,为同时方便三个小区,准备建在BC的垂直平分线上的P点处,建立坐标系如图,且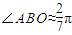 .
.