题目内容
18.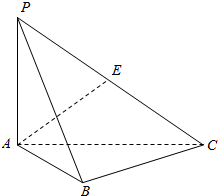 己知三棱锥P-ABC,PA⊥底面ABC,PA=AB=BC=2,直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$.
己知三棱锥P-ABC,PA⊥底面ABC,PA=AB=BC=2,直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$.(1)求证:BC⊥平面PAB;
(2)设E为线段PC中点,求异面直线AE与BC所成的角的大小(结果用反三角函数值表示);
(3)设M是三棱锥P-ABC内的动点(包括边界).满足|AM|≤$\sqrt{2}$,求点M所形成的几何体的全面积.
分析 (1)由已知得PA⊥BC,PA⊥AC,从而得AC=2$\sqrt{2}$,进而AB⊥BC,由此能证明BC⊥平面PAB.
(2)以B为原点,BA为x轴,BC为y轴,过B垂直于平面ABC的直线为z轴,建立空间直角坐标系,利用向量法能求出异面直线AE与BC所成的角的大小.
(3)点M所形成的几何体是球面的一部分,作出图形利用数形结合法能求出点M所形成的几何体的全面积.
解答  (1)证明:∵PA⊥底面ABC,PA=AB=BC=2,
(1)证明:∵PA⊥底面ABC,PA=AB=BC=2,
直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$,
∴PA⊥BC,PA⊥AC,
∴tan∠PAC=$\frac{PA}{AC}$=$\frac{2}{AC}=\frac{\sqrt{2}}{2}$,解得AC=2$\sqrt{2}$,
∴AC2=AB2+BC2,∴AB⊥BC,
∵PA∩AB=A,∴BC⊥平面PAB.
(2)解:以B为原点,BA为x轴,BC为y轴,
过B垂直于平面ABC的直线为z轴,建立空间直角坐标系,
则B(0,0,0),C(0,2,0),
A(2,0,0),P(2,0,2),E(1,1,1),
$\overrightarrow{AE}$=(-1,1,1),$\overrightarrow{BC}$=(0,2,0),
设异面直线AE与BC所成的角为θ,
则cosθ=|$\frac{\overrightarrow{AE}•\overrightarrow{BC}}{|\overrightarrow{AE}|•|\overrightarrow{BC}|}$|=|$\frac{2}{2\sqrt{3}}$|=$\frac{\sqrt{3}}{3}$,
∴异面直线AE与BC所成的角的大小为arccos$\frac{\sqrt{3}}{3}$.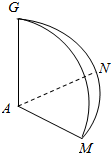
(3)解:点M所形成的几何体如右图,
其中∠NAG=∠MAG=$\frac{π}{2}$,$∠MAN=\frac{π}{4}$,
∴点M所形成的几何体的全面积:
S=$\frac{1}{4}×π×(\sqrt{2})^{2}+\frac{1}{4}×π(\sqrt{2})^{2}+\frac{1}{8}×π×(\sqrt{2})^{2}$+4π×($\sqrt{2}$)2×$\frac{\frac{π}{4}}{2π}×\frac{1}{2}$
=$\frac{π}{2}+\frac{π}{2}+\frac{π}{4}+\frac{1}{2}$
=$\frac{5π}{4}+\frac{1}{2}$.
点评 本题考查线面垂直的证明,考查异面直线所成角的大小的求法,考查几何体的全面积的求法,综合性强,难度大,解题时要认真审题,注意向量法的合理运用.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案各类型家庭生活水平按下表衡量:
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n<59% | 40%≤n<50% | 30%≤n<40% |
| A. | (3,+∞) | B. | [-3,3] | C. | (-3,3) | D. | (-∞,3) |
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-2,0)∪(0,2) |
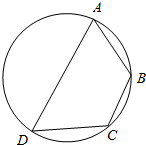 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论: