题目内容
14.设p、q是实数,则表达式u=(p+q)2+($\sqrt{2-{p}^{2}}$-$\frac{9}{q}$)2的最小值为8.分析 u=(p+q)2+($\sqrt{2-{p}^{2}}$-$\frac{9}{q}$)2,表示两点M$(p,\sqrt{2-{p}^{2}})$,N$(-q,\frac{9}{q})$之间的距离的平方.由于点M满足:x2+y2=2,点N满足:xy=-9.设N$(-q,\frac{9}{q})$是曲线xy=-9上的任意一点.利用基本不等式的性质可得:|ON|=$\sqrt{{q}^{2}+\frac{81}{{q}^{2}}}$≥3$\sqrt{2}$,即可得出.
解答  解:要使$\sqrt{2-{p}^{2}}$由意义,则p2≤2.
解:要使$\sqrt{2-{p}^{2}}$由意义,则p2≤2.
u=(p+q)2+($\sqrt{2-{p}^{2}}$-$\frac{9}{q}$)2,表示两点M$(p,\sqrt{2-{p}^{2}})$,N$(-q,\frac{9}{q})$之间的距离的平方.
由于点M满足:x2+y2=2,点N满足:xy=-9.
设N$(-q,\frac{9}{q})$是曲线xy=-9上的任意一点.
则|ON|=$\sqrt{{q}^{2}+\frac{81}{{q}^{2}}}$≥3$\sqrt{2}$,当且仅当q2=9时取等号,
∴M,N两点之间的距离的最小值为3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$.
∴u=(p+q)2+($\sqrt{2-{p}^{2}}$-$\frac{9}{q}$)2的最小值为8.
故答案为:8.
点评 本题考查了曲线上两点之间的距离的最值、两点之间的距离公式、曲线的方程、基本不等式的性质,考查了数形结合思想方法、转化能力与计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
6.函数f(x)=asin2x+b${x}^{\frac{2}{3}}$+c(a,b∈R),若f(-2015)=2013,则f(2015)=( )
| A. | 2018 | B. | -2009 | C. | 2013 | D. | -2013 |
6.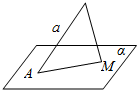 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )| A. | 线段 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
5.已知f(x)在定义域(-4,1)上是减函数,且f(1+a)<f(3a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |
1.集合A={a,b},其中非空真子集个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |