题目内容
已知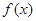 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, .
.
(1)求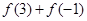 ;
;
(2)求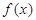 的解析式;
的解析式;
(3)若 ,求区间
,求区间 .
.
(1) ;(2)
;(2) ;(3)区间
;(3)区间 为
为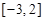 .
.
解析试题分析:(1) ∵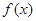 是奇函数,,∴
是奇函数,,∴ ,∴
,∴ ,
,
∴ ;
;
(2)只需要求出 的解析式即可,利用奇函数
的解析式即可,利用奇函数 ,所以设
,所以设 ,则
,则 ,则
,则 ,再与
,再与 的解析式和在一起,写出分段函数;
的解析式和在一起,写出分段函数;
(3)本题是已知函数的值域求定义域问题,根据函数图象可得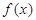 在
在 上单调递增,分别讨论
上单调递增,分别讨论 ,
, 来求解,当
来求解,当 时,
时, 解得
解得 ;当
;当 时,
时, 解得
解得 ;所以区间
;所以区间 为
为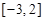 .
.
试题解析:(1)∵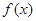 是奇函数,
是奇函数,
∴ 3分
3分
(2)设 ,则
,则 ,∴
,∴
∵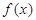 为奇函数,∴
为奇函数,∴ 5分
5分
∴ 6分
6分
(3)根据函数图象可得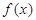 在
在 上单调递增 7分
上单调递增 7分
当 时,
时, 解得
解得 9分
9分
当 时,
时, 解得
解得 11分
11分
∴区间 为
为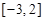 . 12分
. 12分
考点:本题考查函数的性质(奇函数);函数的解析式;函数的定义域和值域.

练习册系列答案
相关题目
 (x≠a).
(x≠a). 的定义域为
的定义域为 .设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
.设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N. 是定值;
是定值; 有最大值还是最小值,并求出此最大值或最小值.
有最大值还是最小值,并求出此最大值或最小值. 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 ,
, .
.  为奇函数,求实数
为奇函数,求实数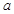 的值;
的值; 上的所有上界构成的集合;
上的所有上界构成的集合; 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时有
时有 .
.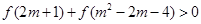 ,求
,求 的取值范围.
的取值范围. ,
, ,求方程
,求方程 的根;
的根; 满足
满足 ,求函数在
,求函数在 的值域.
的值域. 是定义在(-1,1)上的奇函数,其中
是定义在(-1,1)上的奇函数,其中 ,a为正整数,且满足
,a为正整数,且满足 .
. 的解析式;
的解析式; 的
的 的范围;
的范围;