题目内容
如图,在矩形ABCD中,已知AB=3, AD=1, E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: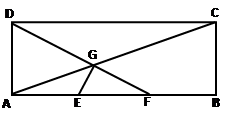
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G ⊥D F。
(1)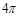 (2)以A为原点,AB所在直线为x轴,建立平面直角坐标系,由A(0,0).C(3,1)知直线AC的方程为:x-3y=0,由D(0,1).F(2,0)知直线DF的方程为:x+2y-2=0,由
(2)以A为原点,AB所在直线为x轴,建立平面直角坐标系,由A(0,0).C(3,1)知直线AC的方程为:x-3y=0,由D(0,1).F(2,0)知直线DF的方程为:x+2y-2=0,由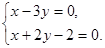 得
得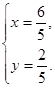 故点G点的坐标为
故点G点的坐标为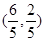 故
故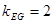 ,
,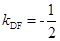 所以
所以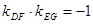 。 即证得:
。 即证得: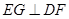
解析试题分析:以A为原点,AB所在直线为x轴,建立平面直角坐标系。 
则A(0,0).B(3,0).C(3,1).
D(0,1).E(1,0).F(2,0)。 1分
(1)设M(x,y), 由题意知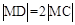 2分
2分
∴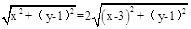 3分
3分
两边平方化简得: ,即
,即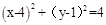 5分
5分
即动点M的轨迹为圆心(4,1),半径为2的圆,
∴动点M的轨迹围成区域的面积为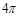 6分
6分
(2)由A(0,0).C(3,1)知直线AC的方程为:x-3y=0, 7分
由D(0,1).F(2,0)知直线DF的方程为:x+2y-2=0, 8分
由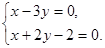 得
得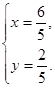 故点G点的坐标为
故点G点的坐标为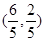 。 10分
。 10分
又点E的坐标为(1,0),故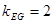 ,
,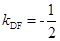 12分
12分
所以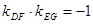 。 即证得:
。 即证得: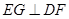 13分
13分
考点:动点的轨迹及直线垂直的判定
点评:求动点的轨迹方程的步骤:建系设点,找到动点满足的关系式并坐标化,化简得方程,验证是否有不满足要求的点。判定两线垂直可利用坐标法判定直线斜率之积为

练习册系列答案
相关题目
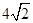 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。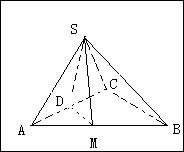
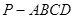 中,
中,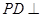 底面
底面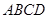 ,面
,面 为侧棱
为侧棱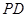 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 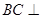 平面
平面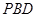 ;
; 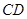 上是否存在点
上是否存在点 ,使
,使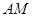 与
与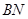 所成角的余弦值为
所成角的余弦值为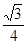 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点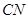 的长;若不存在,说明理由.
的长;若不存在,说明理由.
 平面ABCD,
平面ABCD, ,E是PC上的一点.
,E是PC上的一点.
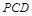 ;
;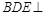 平面
平面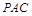 ;
; 为多长时,
为多长时, 平面
平面 ?
?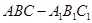 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,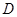 为
为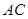 的中点.
的中点.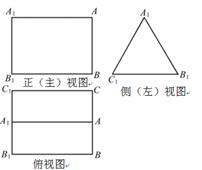
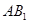 ∥平面
∥平面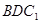 ;
;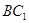 ,且
,且 ,求点
,求点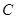 到平面
到平面 的距离.
的距离. 中,
中, 是
是 的中点.
的中点.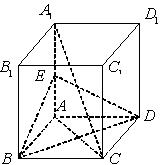
 平面
平面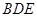 ;
;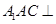 平面
平面 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.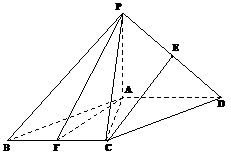
 为圆
为圆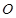 的直径,点
的直径,点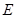 、
、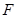 在圆
在圆 所在的平面和圆
所在的平面和圆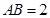 ,
, .
.
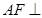 平面
平面 ;
; 的体积.
的体积. 中,
中, ,
, ,
, 为
为 中点.(Ⅰ)证明:
中点.(Ⅰ)证明: ;(Ⅱ)求
;(Ⅱ)求 与平面
与平面 所成角的正弦值;(Ⅲ)在棱
所成角的正弦值;(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使得
,使得