题目内容
已知函数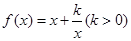 ,
,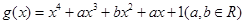 ,(1)若
,(1)若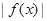 的最小值为2,求
的最小值为2,求 值;(2)设函数
值;(2)设函数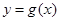 有零点,求
有零点,求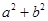 的最小值.
的最小值.
(1)1;(2)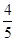 .
.
解析试题分析:(1)本小题可利用对勾函数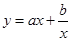 (a>0,b>0)的性质:当
(a>0,b>0)的性质:当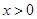 时,在x=
时,在x= 时,取最小值
时,取最小值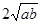 完成求值;(2)本小题等价于方程
完成求值;(2)本小题等价于方程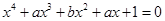 有实根时求
有实根时求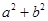 的最小值问题,令
的最小值问题,令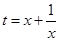 ,问题可化为方程
,问题可化为方程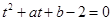 (
(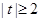 )有实根问题.
)有实根问题.
试题解析:(1)因为函数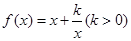 为对勾函数,而
为对勾函数,而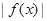 为偶函数,所以只需把问题转化为考虑
为偶函数,所以只需把问题转化为考虑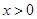 时,
时,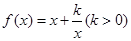 有最小值为2,求
有最小值为2,求 值问题,令
值问题,令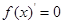 ,可得
,可得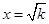 ,代入
,代入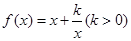 中,有
中,有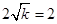 ,得
,得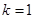 .
.
(2)等价于方程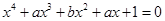 有实根,x=0显然不是根.令
有实根,x=0显然不是根.令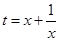 , x为实数,则
, x为实数,则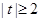 ,同时有:
,同时有: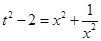 ,方程两边同时除以
,方程两边同时除以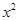 ,得:
,得: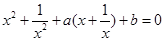 ,即
,即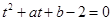 ,此方程有根
,此方程有根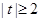 ,令
,令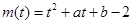 ,有根则
,有根则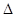 =
= -4(b-2)
-4(b-2) 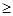 0,若根都在(-2,2),则有
0,若根都在(-2,2),则有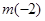 =2-2a+b>0,
=2-2a+b>0, 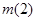 =2+2a+b>0, 即
=2+2a+b>0, 即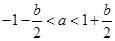 , 也可表为
, 也可表为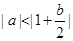 ,故
,故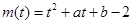 有
有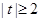 的根的范围是:
的根的范围是: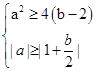 , 即
, 即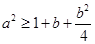 ,故
,故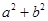
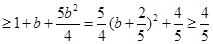 ,当b=
,当b= 时,a=
时,a=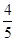 时,
时, 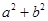 取得最小值
取得最小值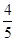 .
.
(另解:由于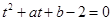 ,则
,则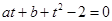 ,从而,
,从而,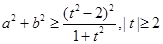 令
令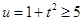 ,从而
,从而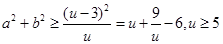 ,从而
,从而 .当且仅当
.当且仅当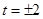 取等号.故
取等号.故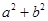 的最小值为
的最小值为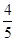 .
.
考点:对勾函数性质,函数的零点,一元二次方程根的分布问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,n台机器人M1,M2,……,Mn位于一条直线上,检测台M在线段M1 Mn上,n台机器人需把各自生产的零件送交M处进行检测,送检程序设定:当Mi把零件送达M处时,Mi+1即刻自动出发送检(i=1,2,……,n-1)已知Mi的送检速度为V(V>0), 且 记
记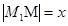 ,n台机器人送检时间总和为f(x).
,n台机器人送检时间总和为f(x).
 |
(1)求f(x)的表达式;
(2)当n=3时,求x的值使得f(x)取得最小值;
(3)求f(x)取得最小值时,x的取值范围.
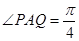 (其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设
(其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设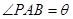 ,搜索区域的面积为
,搜索区域的面积为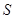 .
.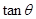 的关系式,并指出
的关系式,并指出 的取值范围;
的取值范围;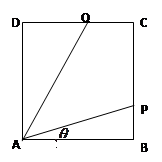
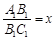 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;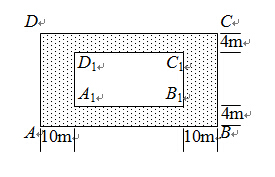
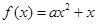
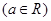
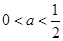 时,
时,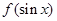
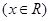 的最大值为
的最大值为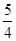 ,求
,求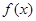 的最小值;
的最小值; ,总有
,总有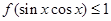 ,试求
,试求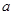 的取值范围.
的取值范围.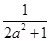 对称,求b的最小值.
对称,求b的最小值.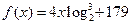 ,则
,则 __
__ ______________.
______________.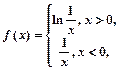 则
则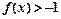 的解集为________.
的解集为________.