题目内容
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000m2,人行道的宽分别为4m和10m(如图所示).
(1)若设休闲区的长和宽的比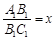 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽应如何设计?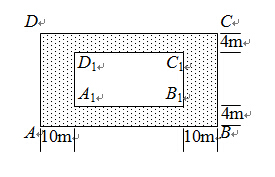
(1) 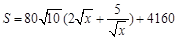 (2) 要使公园所占面积最小,休闲区
(2) 要使公园所占面积最小,休闲区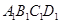 应设计为长100米,宽40米
应设计为长100米,宽40米
解析试题分析:(1)设休闲区的宽为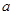 米,则其长为
米,则其长为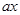 米,根据休闲区
米,根据休闲区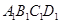 的面积为4000平方米,
的面积为4000平方米,
将 用
用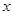 表示,然后根据矩形的面积公式求出公园
表示,然后根据矩形的面积公式求出公园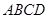 所占面积
所占面积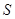 关于
关于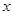 的函数即可;
的函数即可;
(2)利用均值不等式求出最小值,利用等号成立的条件,从而求出长和宽.
试题解析:(1)解:设休闲区的宽为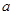 米,则其长为
米,则其长为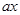 米.
米.
由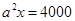 ,得:
,得: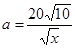 ,则
,则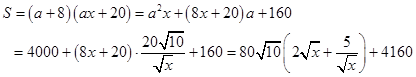
即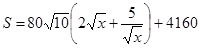 .
.
(2)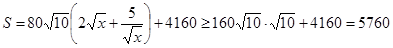
当且仅当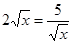 ,即
,即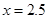 时取等号,此时
时取等号,此时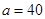 ,
,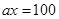 ;
;
所以要使公园所占面积最小,休闲区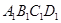 应设计为长100米,宽40米.
应设计为长100米,宽40米.
考点:函数解析式的求法;均值不等式的应用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
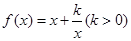 ,
,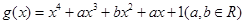 ,(1)若
,(1)若 的最小值为2,求
的最小值为2,求 值;(2)设函数
值;(2)设函数 有零点,求
有零点,求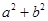 的最小值.
的最小值.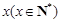 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为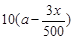 万元
万元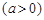 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高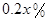 .
.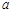 的取值范围是多少?
的取值范围是多少? 的定义域为集合
的定义域为集合 ,关于
,关于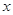 的不等式
的不等式 的解集为
的解集为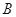 ,若
,若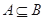 ,求实数
,求实数 的取值范围.
的取值范围. 是
是 上的奇函数,且当
上的奇函数,且当 时,
时, .
.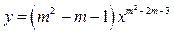 是幂函数,且在
是幂函数,且在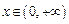 上为减函数, 则实数m的值为_________
上为减函数, 则实数m的值为_________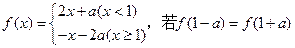 ,则a的
,则a的