题目内容
已知点P1(2,3)、P2(-4,5)和A(-1,2),求过点A且与点P1、P2距离相等的直线方程.
y-2=- (x+1)或x=-1.
(x+1)或x=-1.
 (x+1)或x=-1.
(x+1)或x=-1.(解法1)设所求直线方程为y-2=k(x+1),即kx-y+k+2=0.由点P1、P2到直线的距离相等得 .化简得
.化简得 ,
,
则有3k-1=-3k-3或3k-1=3k+3,
解得k=- 或方程无解.
或方程无解.
方程无解表明这样的k不存在,但过点A,所以直线方程为x=-1,它与P1、P2的距离都是3.
∴所求直线方程为y-2=- (x+1)或x=-1.
(x+1)或x=-1.
(解法2)设所求直线为l,由于l过点A且与P1、P2距离相等,所以l有两种情况,如下图:

①当P1、P2在l的同侧时,有l∥P1P2,此时可求得l的方程为y-2= (x+1),即y-2=-
(x+1),即y-2=- (x+1);
(x+1);
②当P1、P2在l的异侧时,l必过P1、P2的中点(-1,4),此时l的方程为x=-1.
∴所求直线的方程为y-2=- (x+1)或x=-1.
(x+1)或x=-1.
 .化简得
.化简得 ,
,则有3k-1=-3k-3或3k-1=3k+3,
解得k=-
 或方程无解.
或方程无解.方程无解表明这样的k不存在,但过点A,所以直线方程为x=-1,它与P1、P2的距离都是3.
∴所求直线方程为y-2=-
 (x+1)或x=-1.
(x+1)或x=-1.(解法2)设所求直线为l,由于l过点A且与P1、P2距离相等,所以l有两种情况,如下图:

①当P1、P2在l的同侧时,有l∥P1P2,此时可求得l的方程为y-2=
 (x+1),即y-2=-
(x+1),即y-2=- (x+1);
(x+1);②当P1、P2在l的异侧时,l必过P1、P2的中点(-1,4),此时l的方程为x=-1.
∴所求直线的方程为y-2=-
 (x+1)或x=-1.
(x+1)或x=-1.
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 的直线都可以用方程
的直线都可以用方程 表示
表示 的直线都可以用方程
的直线都可以用方程 表示
表示 ,
,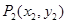 的直线都可以用方程
的直线都可以用方程 表示
表示 表示
表示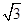 )处的切线方程为________.
)处的切线方程为________.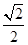
 且垂直于直线
且垂直于直线 的直线
的直线 的方程为 .
的方程为 . ,则直线l的方程为________.
,则直线l的方程为________.