题目内容
已知椭圆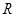 :
: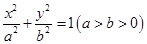 的长轴长为4,且过点
的长轴长为4,且过点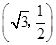 .
.
(1)求椭圆 的方程;
的方程;
(2)设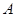 、
、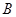 、
、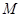 是椭圆上的三点,若
是椭圆上的三点,若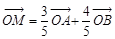 ,点
,点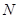 为线段
为线段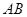 的中点,
的中点,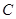 、
、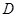 两点的坐标分别为
两点的坐标分别为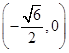 、
、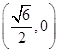 ,求证:
,求证: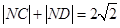 .
.
 :
: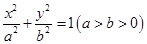 的长轴长为4,且过点
的长轴长为4,且过点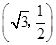 .
.(1)求椭圆
 的方程;
的方程;(2)设
 、
、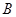 、
、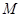 是椭圆上的三点,若
是椭圆上的三点,若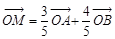 ,点
,点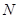 为线段
为线段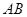 的中点,
的中点,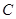 、
、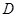 两点的坐标分别为
两点的坐标分别为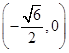 、
、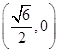 ,求证:
,求证: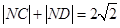 .
.(1) ;(2)详见试题解析.
;(2)详见试题解析.
 ;(2)详见试题解析.
;(2)详见试题解析.试题分析:(1)由已知列方程组可求得
 的值,进而可得椭圆的标准方程;(2)利用平面向量的坐标运算和待定系数法可得线段
的值,进而可得椭圆的标准方程;(2)利用平面向量的坐标运算和待定系数法可得线段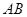 的中点
的中点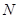 的轨迹是以
的轨迹是以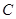
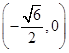 ,
,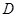
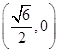 为焦点的椭圆,有椭圆的定义最终可得
为焦点的椭圆,有椭圆的定义最终可得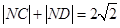 .
.试题解析:(1)由已知
 2分
2分解得
 . 4分
. 4分 椭圆的方程为
椭圆的方程为 . 5分
. 5分(2)设
 ,则
,则 ,
, . 6分
. 6分由
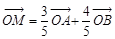 ,
,得
 ,即
,即 . 7分
. 7分
 是椭圆
是椭圆 上一点,所以
上一点,所以
 , 8分
, 8分即

得
 ,故
,故 . 9分
. 9分又线段
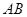 的中点
的中点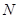 的坐标为
的坐标为 , 10分
, 10分
 ,11分
,11分 线段
线段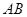 的中点
的中点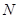
 在椭圆
在椭圆 上. 12分
上. 12分 椭圆
椭圆 的两焦点恰为
的两焦点恰为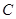
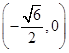 ,
,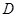
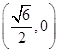 13分
13分
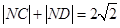 14分
14分
练习册系列答案
相关题目
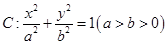 的左右焦点分别为
的左右焦点分别为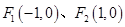 ,且经过点
,且经过点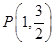 ,
,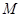 为椭圆上的动点,以
为椭圆上的动点,以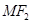 为半径作圆
为半径作圆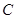 的方程;
的方程;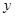 轴有两个交点,求点
轴有两个交点,求点 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.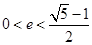 ,
,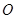 为坐标原点,求证:
为坐标原点,求证: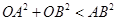 .
. 的离心率为( )
的离心率为( )



 恒有公共点,则实数m的取值范围是( )
恒有公共点,则实数m的取值范围是( )



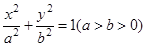 的离心率为
的离心率为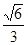 ,且过点
,且过点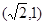 .
. 的直线
的直线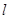 与椭圆相交于不同的两点
与椭圆相交于不同的两点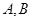 ,试问在
,试问在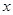 轴上是否存在点
轴上是否存在点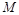 ,使
,使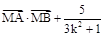 是与
是与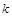 无关的常数?若存在,求出点
无关的常数?若存在,求出点 为椭圆
为椭圆 的两个焦点,P为椭圆上
的两个焦点,P为椭圆上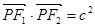 ,则此椭圆离心率的取值范围是 ( )
,则此椭圆离心率的取值范围是 ( )

 中,椭圆
中,椭圆 的标准方程为
的标准方程为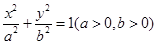 ,右焦点为
,右焦点为 ,右准线为
,右准线为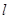 ,短轴的一个端点
,短轴的一个端点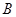 . 设原点到直线
. 设原点到直线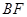 的距离为
的距离为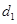 ,
,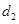 . 若
. 若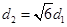 ,则椭圆
,则椭圆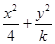 =1的离心率,且e∈(
=1的离心率,且e∈(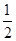 ,1),则实数k的取值范围是 ( )
,1),则实数k的取值范围是 ( ) )
)