题目内容
【题目】已知函数![]() (
(![]() ,
,![]() )的图象与
)的图象与![]() 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位,纵坐标扩大到原来的2倍得到函数
个单位,纵坐标扩大到原来的2倍得到函数![]() 的图象,则下列关于函数
的图象,则下列关于函数![]() 的命题中正确的是( )
的命题中正确的是( )
A.函数![]() 是奇函数B.
是奇函数B.![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.![]() 在
在![]() 上是增函数D.当
上是增函数D.当![]() 时,函数
时,函数![]() 的值域是
的值域是![]()
【答案】C
【解析】
由三角函数恒等变换的公式和三角函数的图象变换,得到![]() ,再结合三角函数的图象与性质,逐项判定,即可求解.
,再结合三角函数的图象与性质,逐项判定,即可求解.
由题意,函数![]() ,
,
因为函数![]() 的图象与
的图象与![]() 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为![]() 的等差数列,
的等差数列,
可得![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,
,
把函数![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位,纵坐标扩大到原来的2倍得到函数
个单位,纵坐标扩大到原来的2倍得到函数![]() 的图象,可得函数
的图象,可得函数![]() ,
,
可得函数![]() 为非奇非偶函数,所以A不正确;
为非奇非偶函数,所以A不正确;
由![]() ,所以
,所以![]() 不是函数的对称轴,所以B不正确;
不是函数的对称轴,所以B不正确;
由![]() ,则
,则![]() ,由正弦函数的性质,可得函数
,由正弦函数的性质,可得函数![]() 在
在![]() 上单调递增,所以C正确;
上单调递增,所以C正确;
由![]() ,则
,则![]() ,
,
当![]() 时,即
时,即![]() ,函数取得最小值,最小值为
,函数取得最小值,最小值为![]() ,
,
当![]() 时,即
时,即![]() ,函数取得最大值,最大值为
,函数取得最大值,最大值为![]() ,
,
所以函数的值域为![]() ,所以D不正确.
,所以D不正确.
故选:C.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 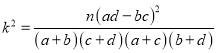 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】某大学为了调查该校学生性别与身高的关系,对该校1000名学生按照![]() 的比例进行抽样调查,得到身高频数分布表如下:
的比例进行抽样调查,得到身高频数分布表如下:
男生身高频率分布表
男生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
(1)估计这1000名学生中女生的人数;
(2)估计这1000名学生中身高在![]() 的概率;
的概率;
(3)在样本中,从身高在![]() 的女生中任取3名女生进行调查,设
的女生中任取3名女生进行调查,设![]() 表示所选3名学生中身高在
表示所选3名学生中身高在![]() 的人数,求
的人数,求![]() 的分布列和数学期望.(身高单位:厘米)
的分布列和数学期望.(身高单位:厘米)