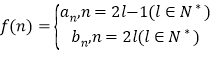题目内容
【题目】已知椭圆C: ![]() (
(![]() >b>0)的左、右顶点分别为A1、A2,上、下顶点分别为B2、B1,O为坐标原点,四边形A1B1A2B2的面积为4,且该四边形内切圆的方程为
>b>0)的左、右顶点分别为A1、A2,上、下顶点分别为B2、B1,O为坐标原点,四边形A1B1A2B2的面积为4,且该四边形内切圆的方程为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若M、N是椭圆C上的两个不同的动点,直线OM、ON的斜率之积等于![]() ,试探求△OMN的面积是否为定值,并说明理由.
,试探求△OMN的面积是否为定值,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)先利用四边形的面积求得![]() ,再利用直线和圆相切进行求解;(Ⅱ)设出直线方程,联立直线和椭圆的方程,得到关于
,再利用直线和圆相切进行求解;(Ⅱ)设出直线方程,联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系、直线的斜率公式和三角形的面积公式进行求解.
的一元二次方程,利用根与系数的关系、直线的斜率公式和三角形的面积公式进行求解.
试题解析:(Ⅰ)∵四边形A1B1A2B2的面积为4,又可知四边形A1B1A2B2为菱形,
∴![]() ,即ab=2①
,即ab=2①
由题意可得直线A2B2方程为:![]() ,即bx+ay﹣ab=0,
,即bx+ay﹣ab=0,
∵四边形A1B1A2B2内切圆方程为![]() ,
,
∴圆心O到直线A2B2的距离为![]() ,即
,即![]() ②
②
由①②解得:a=2,b=1,∴椭圆C的方程为:![]()
(Ⅱ)若直线MN的斜率存在,设直线MN的方程为y=kx+m,M(x1,y1),N(x2,y2),
由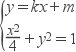 得:(1+4k2)x2+8mkx+4(m2﹣1)=0∵直线l与椭圆C相交于M,N两个不同的点,
得:(1+4k2)x2+8mkx+4(m2﹣1)=0∵直线l与椭圆C相交于M,N两个不同的点,
∴△=64m2k2﹣16(1+4k2)(m2﹣1)>0得:1+4k2﹣m2>0③
由韦达定理:![]()
∵直线OM,ON的斜率之积等于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴2m2=4k2+1满足③…(9分)
∴![]() ,
,
又O到直线MN的距离为![]() ,
,![]() ,
,
所以△OMN的面积![]()
若直线MN的斜率不存在,M,N关于x轴对称
设M(x1,y1),N(x1,﹣y1),则![]() ,
,![]() ,
,
又∵M在椭圆上,![]() ,∴
,∴![]() ,
,
所以△OMN的面积S=![]() =
=![]() =1.
=1.
综上可知,△OMN的面积为定值1.

练习册系列答案
相关题目