题目内容
下列几个命题:
(1)函数f(x)=xn+ax-1(n∈Z,a>0,a≠1)的图象必过点(1,2);
(2)f(x)=
+
是偶函数,但不是奇函数;
(3)函数y=f(x)值域是[-3,3],则函数y=f(x-2)值域是[-1,5];
(4)设函数y=f(x)定义域为R,则函数y=f(1-x)与y=f(x-1)图象关于y轴对称;
(5)y=|3-x2|图象与直线y=a有k个公共点,则k的值不可能是1;
上述五个命题中所有正确的命题序号是
(1)函数f(x)=xn+ax-1(n∈Z,a>0,a≠1)的图象必过点(1,2);
(2)f(x)=
| x2-4 |
| 4-x2 |
(3)函数y=f(x)值域是[-3,3],则函数y=f(x-2)值域是[-1,5];
(4)设函数y=f(x)定义域为R,则函数y=f(1-x)与y=f(x-1)图象关于y轴对称;
(5)y=|3-x2|图象与直线y=a有k个公共点,则k的值不可能是1;
上述五个命题中所有正确的命题序号是
①④⑤
①④⑤
.分析:(1)由f(1)=2即可判断(1)正确;
(2)依题意,可求得x=±2,从而可得f(x)=
+
是偶函数,也是奇函数;
(3)利用函数的性质可知,左右平移不改变其值域,从而可知(3)的正误;
(4)利用1-x+(x-1)=0,即可判断(4)的正误;
(5)在同一直角坐标系中作出曲线y=|3-x2|与直线y=a的图形,分析即可判其正误.
(2)依题意,可求得x=±2,从而可得f(x)=
| x2-4 |
| 4-x2 |
(3)利用函数的性质可知,左右平移不改变其值域,从而可知(3)的正误;
(4)利用1-x+(x-1)=0,即可判断(4)的正误;
(5)在同一直角坐标系中作出曲线y=|3-x2|与直线y=a的图形,分析即可判其正误.
解答:解:(1)∵f(x)=xn+ax-1(n∈Z,a>0,a≠1),
∴f(1)=1n+a1-1=1+1=2,
故函数的图象必过点(1,2),即(1)正确;
(2)由
得4≤x2≤4,即x2=4,x=±2,
∵f(2)=f(-2)=0,f(-2)=-f(2)=0,
∴f(x)=
+
是偶函数,也是奇函数,故(2)错误;
(3)因为函数y=f(x-2)是由函数y=f(x)向右平移2个单位得到的,图象上下没有平移,值域不变,是[-3,3],故(3)错误;
(4)∵1-x+(x-1)=0,函数y=f(x)定义域为R,
∴函数y=f(1-x)与y=f(x-1)图象关于y轴对称,(4)正确;
(5)∵y=|3-x2|,直线y=a有k个公共点,其图象如下,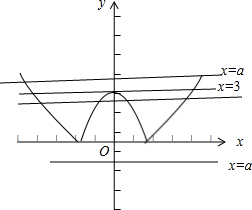
由图知,当a<0时,无公共点;
当a=0或a>3时有两个公共点;
当0<a<3时有四个公共点;
∴y=|3-x2|图象与直线y=a有k个公共点,k的值不可能是1,(5)正确.
综上所述,上述五个命题中所有正确的命题序号是①④⑤.
故答案为:①④⑤.
∴f(1)=1n+a1-1=1+1=2,
故函数的图象必过点(1,2),即(1)正确;
(2)由
|
∵f(2)=f(-2)=0,f(-2)=-f(2)=0,
∴f(x)=
| x2-4 |
| 4-x2 |
(3)因为函数y=f(x-2)是由函数y=f(x)向右平移2个单位得到的,图象上下没有平移,值域不变,是[-3,3],故(3)错误;
(4)∵1-x+(x-1)=0,函数y=f(x)定义域为R,
∴函数y=f(1-x)与y=f(x-1)图象关于y轴对称,(4)正确;
(5)∵y=|3-x2|,直线y=a有k个公共点,其图象如下,

由图知,当a<0时,无公共点;
当a=0或a>3时有两个公共点;
当0<a<3时有四个公共点;
∴y=|3-x2|图象与直线y=a有k个公共点,k的值不可能是1,(5)正确.
综上所述,上述五个命题中所有正确的命题序号是①④⑤.
故答案为:①④⑤.
点评:本题考查命题的真假判断与应用,着重考查的奇偶性与对称性,考查直线与与二次曲线的相交问题,着重考查分析、推理与运算能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
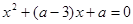 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则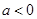 ;
;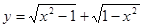 是偶函数,但不是奇函数;
是偶函数,但不是奇函数; 的值域是
的值域是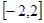 ,则函数
,则函数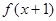 的值域为
的值域为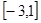 ;
; 和直线
和直线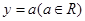 的公共点个数是
的公共点个数是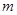 ,则
,则