题目内容
设函数f(x)=|x2-4x-5|.
(1)在区间[-2,6]上画出函数f(x)的图像(如图);
(2)设集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).试判断集合A和B之间的关系,并给出证明;
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图像位于函数f(x)图像的上方.

答案:
解析:
提示:
解析:
|
解:(1)f(x)=|x2-4x-5|=
(2)方程f(x)=5的解分别是x=2 可得f(x)≥5的解是x≤2 则A={x|x≤2 ∵2+ ∴B (3)当x∈[-1,5]时,f(x)=-x2+4x+5.设g(x)=kx+3k-f(x), 则g(x)=kx+3k-(-x2+4x+5)=x2+(k-4)x+(3k-5)=(x ①当-1≤ g(x)min= ∵16≤(k-10)2<64,∴(k-10)2-64<0.则g(x)min>0. ②当 由①②,可知当k>2时,在x∈[-1,5]上,g(x)>0. 因此,在区间[-1,5]上,y=k(x+3)的图像位于函数f(x)图像的上方. |
提示:
|
(1)可以利用对称变换作图法或将函数的解析式化为分段函数;(2)利用图像解不等式f(x)≥5;应用定义证明集合A和B之间的关系;(3)转化为证明:当k>2时,在x∈[-1,5]上,kx+3k-f(x)>0恒成立即可. |

练习册系列答案
相关题目
 其图像如图所示.
其图像如图所示.
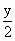 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.