题目内容
三角形 中,
中,  ,以边
,以边 所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )
所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )
A. | B. | C. . . | D. |
A
解析试题分析:因为直角边BC=1,那么可知圆锥的底面的半径为3,高为AB=3,那么结合旋转体的定义可知,圆锥的体积公式V=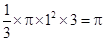 ,故选A
,故选A
考点:本试题主要考查了旋转体中圆锥体积的求解问题。是一道基础试题。
点评:解决该试题的关键是能理解以直角三角形AB为一边,旋转得到是一个圆锥体,那么根据圆锥的体积公式得到。

练习册系列答案
相关题目
下列说法错误的是( )
| A.棱柱的两个底面互相平行 | B.圆台与棱台统称为台体 |
| C.棱柱的侧棱垂直于底面 | D.圆锥的轴截面是一个等腰三角形 |
若正四棱柱 的底面边长为1,
的底面边长为1, 与底面
与底面 成60°角,则
成60°角,则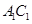 到底面
到底面 的距离为 ( )
的距离为 ( )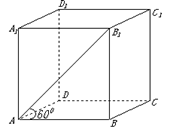
A. | B.1 | C. | D. |
已知某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. |
C. | D. |
已知四面体 的外接球的球心
的外接球的球心 在
在 上,且
上,且 平面
平面 ,
, ,若四面体
,若四面体 的体积为
的体积为 ,则该球的体积为 ( )
,则该球的体积为 ( )
A. | B. | C. | D. |
 中,
中,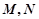 分别是
分别是 的中点,则下列判断错误的是( )
的中点,则下列判断错误的是( ) 与
与 垂直
垂直  垂直
垂直  平行
平行  平行
平行 






 B.
B. C.
C.  D.
D.




