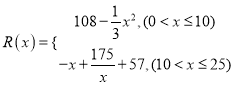题目内容
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
【答案】(1)![]() .(2)
.(2)![]()
【解析】试题分析:(1)求出抛物线的焦点坐标,结合题意列关于p的等式求p,则抛物线方程可求;
(2)由(1)求出M的坐标,设出直线DE的方程![]() ,联立直线方程和抛物线方程,化为关于y的一元二次方程后D,E两点纵坐标的和与积,利用
,联立直线方程和抛物线方程,化为关于y的一元二次方程后D,E两点纵坐标的和与积,利用![]() 得到t与m的关系,进一步得到DE方程,由直线系方程可得直线DE所过定点.
得到t与m的关系,进一步得到DE方程,由直线系方程可得直线DE所过定点.
试题解析:
(1)由题意设抛物线方程为![]() ,
,
其准线方程为![]() ,
,
∵![]() 到焦点的距离等于
到焦点的距离等于![]() 到其准线的距离,
到其准线的距离,
∴![]() ,∴
,∴![]() .
.
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)可得点![]() ,可得直线
,可得直线![]() 的斜率不为0,
的斜率不为0,
设直线![]() 的方程为:
的方程为: ![]() ,
,
联立![]() ,得
,得![]() ,
,
则![]() ①.
①.
设![]() ,则
,则![]() .
.
∵![]()
![]()
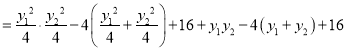
![]()
![]()
即![]() ,得:
,得: ![]() ,
,
∴![]() ,即
,即![]() 或
或![]() ,
,
代人①式检验均满足![]() ,
,
∴直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.
∴直线过定点![]() (定点
(定点![]() 不满足题意,故舍去).
不满足题意,故舍去).
点睛:抛物线的定义是解决抛物线问题的基础,它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化.如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线定义就能解决问题.因此,涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离,这样就可以使问题简单化.

练习册系列答案
相关题目