题目内容
正三棱柱ABC-A1B1C1的所有棱长都为2,则异面直线AB1与BC1所成角的余弦值为
- A.

- B.

- C.

- D.

B
分析:通过建立空间直角坐标系,利用两条异面直线的方向向量的夹角即可得出异面直线所成的角.
解答:如图所示,分别取BC、B1C1的中点O、O1,由正三棱柱的性质可得AO、BO、OO1令两垂直,建立空间直角坐标系.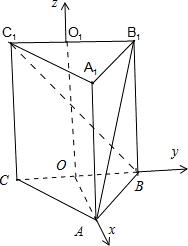
∵所有棱长都为2,∴A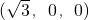 ,B(0,1,0),B1(0,1,2),
,B(0,1,0),B1(0,1,2),
C1(0,-1,2).
∴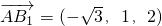 ,
,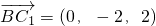
∴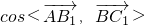 =
=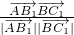 =
=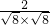 =
= .
.
∴异面直线AB1与BC1所成角的余弦值为 .
.
故选B.
点评:熟练掌握通过建立空间直角坐标系并利用两条异面直线的方向向量的夹角得出异面直线所成的角的方法是解题的关键.
分析:通过建立空间直角坐标系,利用两条异面直线的方向向量的夹角即可得出异面直线所成的角.
解答:如图所示,分别取BC、B1C1的中点O、O1,由正三棱柱的性质可得AO、BO、OO1令两垂直,建立空间直角坐标系.

∵所有棱长都为2,∴A
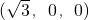 ,B(0,1,0),B1(0,1,2),
,B(0,1,0),B1(0,1,2),C1(0,-1,2).
∴
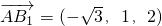 ,
,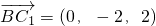
∴
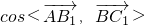 =
=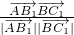 =
=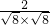 =
= .
.∴异面直线AB1与BC1所成角的余弦值为
 .
.故选B.
点评:熟练掌握通过建立空间直角坐标系并利用两条异面直线的方向向量的夹角得出异面直线所成的角的方法是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.