题目内容
已知二次函数f(x)=ax2+|a-1|x+a.(1)函数f(x)在(-∞,-1)上单调递增,求实数a的取值范围;
(2)关于x不等式
 ≥2在x∈[1,2]上恒成立,求实数a的取值范围;
≥2在x∈[1,2]上恒成立,求实数a的取值范围;(3)函数g(x)=f(x)+
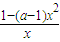 在(2,3)上是增函数,求实数a的取值范围.
在(2,3)上是增函数,求实数a的取值范围.
【答案】分析:(1)分a>0,a<0两种情况求出二次函数f(x)的增区间,使(-∞,-1)为增区间的子集即可;
(2)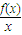 ≥2在x∈[1,2]上恒成立,等价于在[1,2]上
≥2在x∈[1,2]上恒成立,等价于在[1,2]上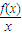 的最小值大于等于2,利用导数即可求得其最小值;
的最小值大于等于2,利用导数即可求得其最小值;
(3)设2<x1<x2<3,则g(x1)<g(x2)恒成立,分离出参数a后转化为求函数最值即可解决;
解答:解:显然a≠0(1)若a>0,f(x)的增区间为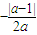 ,+∞),而函数f(x)在(-∞,-1)上单调递增,不符合题意;
,+∞),而函数f(x)在(-∞,-1)上单调递增,不符合题意;
若a<0,则f(x)=ax2+(1-a)x+a,其增区间为(-∞,-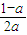 ).
).
又f(x)在(-∞,-1)上单调递增,所以有- ≥-1,解得a
≥-1,解得a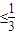 ,
,
故a<0,所以实数a的取值范围为:a<0.
(2)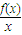 ≥2即ax+
≥2即ax+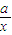 +|a-1|≥2,令g(x)=ax+
+|a-1|≥2,令g(x)=ax+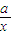 +|a-1|,
+|a-1|,
则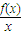 ≥2在x∈[1,2]上恒成立,等价于gmin(x)≥2,
≥2在x∈[1,2]上恒成立,等价于gmin(x)≥2,
g′(x)=a-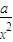 =
=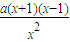 ,
,
①当a>0时,x∈[1,2],g′(x)≥0,g(x)在[1,2]上递增,
gmin(x)=g(1)=2a+|a-1|≥2,解得a≥1;
②当a<0时,g′(x)≤0,此时g(x)在[1,2]上递减,
gmin(x)=g(2)=2a+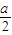 +|a-1|=
+|a-1|= a+1≥2,解得a
a+1≥2,解得a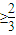 ,(舍)
,(舍)
综上,实数a的取值范围为a≥1.
(3)g(x)=ax2+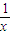 +a在(2,3)上是增函数,
+a在(2,3)上是增函数,
设2<x1<x2<3,则g(x1)<g(x2),
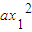 +
+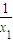 +a<
+a<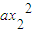 +
+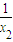 +a,a(x1+x2)(x1-x2)<
+a,a(x1+x2)(x1-x2)<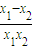 ,
,
因为2<x1<x2<3,所以a>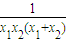 ,
,
而 ∈(
∈(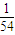 ,
,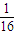 ),
),
所以a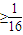 .
.
点评:本题考查二次函数的单调性及函数恒成立问题,考查分类讨论思想,考查学生灵活运用所学知识分析解决问题的能力,属中档题.
(2)
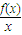 ≥2在x∈[1,2]上恒成立,等价于在[1,2]上
≥2在x∈[1,2]上恒成立,等价于在[1,2]上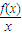 的最小值大于等于2,利用导数即可求得其最小值;
的最小值大于等于2,利用导数即可求得其最小值;(3)设2<x1<x2<3,则g(x1)<g(x2)恒成立,分离出参数a后转化为求函数最值即可解决;
解答:解:显然a≠0(1)若a>0,f(x)的增区间为
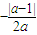 ,+∞),而函数f(x)在(-∞,-1)上单调递增,不符合题意;
,+∞),而函数f(x)在(-∞,-1)上单调递增,不符合题意;若a<0,则f(x)=ax2+(1-a)x+a,其增区间为(-∞,-
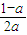 ).
).又f(x)在(-∞,-1)上单调递增,所以有-
 ≥-1,解得a
≥-1,解得a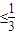 ,
,故a<0,所以实数a的取值范围为:a<0.
(2)
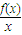 ≥2即ax+
≥2即ax+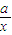 +|a-1|≥2,令g(x)=ax+
+|a-1|≥2,令g(x)=ax+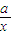 +|a-1|,
+|a-1|,则
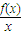 ≥2在x∈[1,2]上恒成立,等价于gmin(x)≥2,
≥2在x∈[1,2]上恒成立,等价于gmin(x)≥2,g′(x)=a-
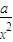 =
=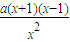 ,
,①当a>0时,x∈[1,2],g′(x)≥0,g(x)在[1,2]上递增,
gmin(x)=g(1)=2a+|a-1|≥2,解得a≥1;
②当a<0时,g′(x)≤0,此时g(x)在[1,2]上递减,
gmin(x)=g(2)=2a+
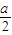 +|a-1|=
+|a-1|= a+1≥2,解得a
a+1≥2,解得a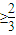 ,(舍)
,(舍)综上,实数a的取值范围为a≥1.
(3)g(x)=ax2+
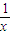 +a在(2,3)上是增函数,
+a在(2,3)上是增函数,设2<x1<x2<3,则g(x1)<g(x2),
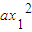 +
+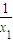 +a<
+a<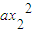 +
+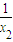 +a,a(x1+x2)(x1-x2)<
+a,a(x1+x2)(x1-x2)<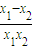 ,
,因为2<x1<x2<3,所以a>
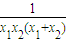 ,
,而
 ∈(
∈(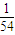 ,
,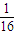 ),
),所以a
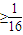 .
.点评:本题考查二次函数的单调性及函数恒成立问题,考查分类讨论思想,考查学生灵活运用所学知识分析解决问题的能力,属中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目