题目内容
已知构成某系统的元件能正常工作的概率为p(0＜p＜1)，且各个元件能否正常工作是相互独立的．今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙．
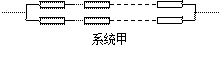
（1）试分别求出系统甲、乙能正常工作的概率p1，p2；
（2）比较p1与p2的大小，并从概率意义上评价两系统的优劣．
（1）试分别求出系统甲、乙能正常工作的概率p1，p2；
（2）比较p1与p2的大小，并从概率意义上评价两系统的优劣．
略
解：（1）p1＝pn(2－pn)， ……………………2分
p2＝pn(2－p)n； ……………………4分
（2）(用二项式定理证明)
p2－p1＝pn{[1＋(1－p)]n－2＋[1－(1－p)]n
＝pn{[1＋C(1－p)＋C(1－p)2＋C(1－p)3＋…＋C(1－p)n]－2
＋[1－C(1－p)＋C(1－p)2－C(1－p)3＋…＋(－1)nC(1－p)n]}
＝pn[C(1－p)2＋C(1－p)4＋…]＞0． …………………10分
说明：作差后化归为用数学归纳法证明：(2－p)n＞2－pn也可．
p2＝pn(2－p)n； ……………………4分
（2）(用二项式定理证明)
p2－p1＝pn{[1＋(1－p)]n－2＋[1－(1－p)]n
＝pn{[1＋C(1－p)＋C(1－p)2＋C(1－p)3＋…＋C(1－p)n]－2
＋[1－C(1－p)＋C(1－p)2－C(1－p)3＋…＋(－1)nC(1－p)n]}
＝pn[C(1－p)2＋C(1－p)4＋…]＞0． …………………10分
说明：作差后化归为用数学归纳法证明：(2－p)n＞2－pn也可．
练习册系列答案
相关题目
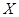，则P（
孩，把她们分别记为A，C，J，K，S。她们应聘秘书工作，但只有3个秘书职位，因此5人中仅有三人被录用。如果5人被录用的机会
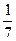
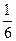
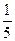
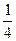
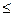y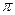
},集合B={(x,y)|(x-2)
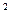+(y-2)
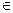A的概率是 。