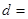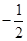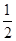题目内容
已知{an}为等差数列,且a3=-6,a6=0.
(1)求{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求{bn}的前n项和公式.
(1)求{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求{bn}的前n项和公式.
解:(1)an=2(n-6)=2n-12
(2)bn =-8,则前n项和为-8n..
(2)bn =-8,则前n项和为-8n..
本试题主要是考查了等差数列的通项公式的求解和等比数列的求和的运用。
(1)因为{an}为等差数列,且a3=-6,a6=0.,3d=6,d=2,从而得到通项公式。
(2)由题意可得:b1=-8,b2=a1+a2+a3,=3 a2=-8,从而得到公比,然后得到求和。
(1)因为{an}为等差数列,且a3=-6,a6=0.,3d=6,d=2,从而得到通项公式。
(2)由题意可得:b1=-8,b2=a1+a2+a3,=3 a2=-8,从而得到公比,然后得到求和。

练习册系列答案
相关题目
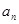 }中,
}中,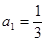 ,并且对任意
,并且对任意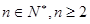 都有
都有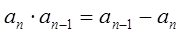 成立,令
成立,令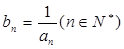 .
.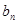 }的通项公式;
}的通项公式;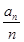 }的前n项和为
}的前n项和为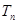 ,证明:
,证明: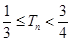
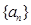 的前
的前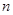 项和
项和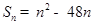 。
。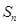 的最大或最小值。
的最大或最小值。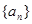 中,
中, ,则数列
,则数列 等于
等于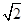
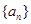 的公差为
的公差为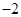 ,且
,且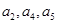 成等比数列,则
成等比数列,则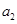 等于 ( )
等于 ( )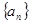 的公差为2,若
的公差为2,若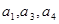 成等比数列, 则
成等比数列, 则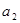 = ( )
= ( )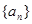 和
和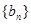 的前n项和分别为
的前n项和分别为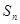 和
和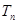 ,对一切自然数n,都有
,对一切自然数n,都有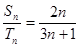 ,则
,则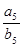 等于 ( )
等于 ( )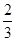
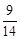
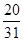
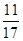
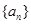 是等差数列,且
是等差数列,且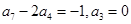 ,则公差
,则公差