题目内容
某个体服装店经营某种服装,一周内获纯利y(元)与该周每天销售这种服装的件数x之间的一组数据如下:
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知![]() =280,
=280, ![]() =45 309,
=45 309, ![]() =3 487,此时r0.05=0.754.
=3 487,此时r0.05=0.754.
(1)求![]() ,
,![]() ;
;
(2)判断一周内获纯利润y与该周每天销售件数x之间是否线性相关,如果线性相关,求出回归直线方程.
(1)![]() =6,
=6,![]() =≈79.86.(2)
=≈79.86.(2)![]() =4.746x+51.386
=4.746x+51.386
解析:
(1)![]() =
=![]() (3+4+5+6+7+8+9)=6,
(3+4+5+6+7+8+9)=6,![]() =
=![]() (66+69+73+81+89+90+91)≈79.86.
(66+69+73+81+89+90+91)≈79.86.
(2)根据已知![]() =280,
=280, ![]() =45 309,
=45 309, ![]() =3 487,
=3 487,
得相关系数
r=![]() ≈0.973.
≈0.973.
由于0.973>0.754,所以纯利润y与每天销售件数x之间具有显著线性相关关系.
利用已知数据可求得回归直线方程为![]() =4.746x+51.386.
=4.746x+51.386.

练习册系列答案
相关题目
某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表:
(1)求纯利y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装13件,估计可获纯利多少元?
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
(2)若该周内某天销售服装13件,估计可获纯利多少元?
某个体服装店经营某种服装,在某周内获利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求
 (2)、
(2)、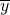 (3);
(3);(2)请画出上表数据的散点图;
(3)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=
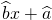 ;(精确到0.01)
;(精确到0.01)(4)若该周内某天销售服装20件,估计可获利多少元.



 ;
;