题目内容
某个体服装店经营某种服装，在某周内获纯利y（元）与该周每天销售这种服装件数x之间的一组数据关系如下表：| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
（2）若该周内某天销售服装13件，估计可获纯利多少元？
分析：（1）求出利用最小二乘法来求线性回归方程的系数的量，求出横标和纵标的平均数，求出系数，再求出a的值，注意运算不要出错；
（2）由回归直线方程预测，该周内某天销售服装13件，估计可获利多少元，只需将x=13代入求解即可．
（2）由回归直线方程预测，该周内某天销售服装13件，估计可获利多少元，只需将x=13代入求解即可．
解答：解：（1）
=
=6，
=80， y与x具有线性相关关系，
3×66+4×69+5×73+6×81+7×89+8×90+9×91=3487，32+42+52+62+72+82+92=280，
设回归方程
=bx+
，∴b=
=
，
∴回归方程为
=
(x-6)+80，
（2）当x=13时，
=
(13-6)+80=113，
故该周内某天的销售量为13件，估计这天可获纯利大约为113元．
| x |
| 3+4+5+6+7+8+9 |
| 7 |
| y |
3×66+4×69+5×73+6×81+7×89+8×90+9×91=3487，32+42+52+62+72+82+92=280，
设回归方程
 |
| y |
|
| a |
| 3487-7×6×80 |
| 280-7×36 |
| 33 |
| 7 |
∴回归方程为
|
| y |
| 33 |
| 7 |
（2）当x=13时，
|
| y |
| 33 |
| 7 |
故该周内某天的销售量为13件，估计这天可获纯利大约为113元．
点评：本题考查线性回归方程的求法和应用，本题解题的关键是利用最小二乘法做出线性回归方程的系数，本题是一个近几年可能出现在高考卷中的题目．
练习册系列答案
相关题目
某个体服装店经营某种服装，一周内获纯利y（元）与该周每天销售这种服装的件数x之间的一组数据如下：
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知
=280, 
=45 309, 
=3 487,此时r0.05=0.754.
（1）求
,
;
（2）判断一周内获纯利润y与该周每天销售件数x之间是否线性相关，如果线性相关，求出回归直线方程.
；某个体服装店经营某种服装，在某周内获利y（元）与该周每天销售这种服装件数x之间的一组数据关系如下表
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
（1）求
（2）、
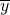（3）；（2）请画出上表数据的散点图；
（3）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y=
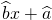；（精确到0.01）（4）若该周内某天销售服装20件，估计可获利多少元．