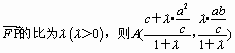题目内容

已知椭圆C的方程为(a＞b＞0)，双曲线的两条渐近线为l1，l2，过椭圆C的右焦点F作直线l，使l⊥l1，又l与l2交于P点，设l与椭圆C的两个交点由上至下依次为A、B(如图)．

(1)

当l1与l2夹角为60°，双曲线焦距为4时，求椭圆C的方程和离心率．

(2)

求的最大值．

答案：
解析：

(1)

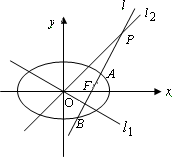
∵双曲线的渐近线为y＝±，两渐近线夹角为60°

又

∴∠POX＝30°，∴＝tan30°＝，∴a＝b……………………2分

又c＝2，a2＋b2＝c2，∴3b2＋b2＝4．

∴b2＝1，a2＝3…………………………………………(4分)

∴椭圆C的方程为，离心率．……………………6分

(2)

由已知l：y＝，与y＝联立，解得P()　　 ……………………7分

∴P在椭圆的右准线上，又A在线段FP上，

设A分

将A点坐标代入椭圆方程，得

等式两边同除以a4，

∴≤－2

∴当2－

即的最大值为……………………14分


练习册系列答案
相关题目
已知椭圆C的方程为
x2
a2
+
y2
b2
=1(a≥2b＞0)．
（1）求椭圆C的离心率的取值范围；
（2）若椭圆C与椭圆2x2+5y2=50有相同的焦点，且过点M（4，1），求椭圆C的标准方程．
已知椭圆C的方程为
x2
a2
+ 
y2
b2
=1（a＞b＞0），称圆心在坐标原点O，半径为
a2+b2
的圆为椭圆C的“伴随圆”，椭圆C的短轴长为2，离心率为
6
3
．
（Ⅰ）求椭圆C及其“伴随圆”的方程；
（Ⅱ）若直线l与椭圆C交于A，B两点，与其“伴随圆”交于C，D两点，当|CD|=
13
 时，求△AOB面积的最大值．
（2012•泉州模拟）已知椭圆C的方程为：
x2
a2
+
y2
2
=1 (a＞0)，其焦点在x轴上，离心率e=
2
2
．
（1）求该椭圆的标准方程；
（2）设动点P（x0，y0）满足
OP
=
OM
+2
ON
，其中M，N是椭圆C上的点，直线OM与ON的斜率之积为-
1
2
，求证：x02+2
y
2
0
为定值．
（3）在（2）的条件下，问：是否存在两个定点A，B，使得|PA|+|PB|为定值？若存在，给出证明；若不存在，请说明理由．
（2012•衡阳模拟）已知椭圆C的方程为
y2
a2
+
x2
b2
=1（a＞b＞0），离心率e=
2
2
，上焦点到直线y=
a2
c
的距离为
2
2
，直线l与y轴交于一点P（0，m），与椭圆C交于相异两点A，B且
AP
=t
PB
．
（1）求椭圆C的方程；
（2）若
OA
+t
OB
=4
OP
，求m的取值范围•
已知椭圆C的方程为
x 2
4
+
y2
3
=1，过C的右焦点F的直线与C相交于A、B两点，向量
m
=(-1，-4)，若向量
OA
-
OB
与
m
-
OF
共线，则直线AB的方程是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网