题目内容
P为直线y=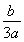 x与双曲线
x与双曲线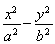 =1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=________.
=1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=________.

【解析】由 得
得 又PF1垂直于x轴,所以
又PF1垂直于x轴,所以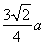 =c,即离心率为e=
=c,即离心率为e= .
.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
P为直线y=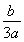 x与双曲线
x与双曲线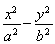 =1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=________.
=1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=________.

【解析】由 得
得 又PF1垂直于x轴,所以
又PF1垂直于x轴,所以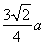 =c,即离心率为e=
=c,即离心率为e= .
.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案