题目内容
6.若不等式(x-a)2<1成立的充分不必要条件是$\frac{1}{2}$<x<$\frac{3}{2}$,则实数a的取值范围是( )| A. | $\frac{1}{2}$<a<$\frac{3}{2}$ | B. | $\frac{1}{2}$≤a≤$\frac{3}{2}$ | C. | a<$\frac{1}{2}$或a>$\frac{3}{2}$ | D. | a≤$\frac{1}{2}$或a≥$\frac{3}{2}$ |
分析 不等式(x-a)2<1,解得:a-1<x<a+1.由于不等式(x-a)2<1成立的充分不必要条件是$\frac{1}{2}$<x<$\frac{3}{2}$,可得$\left\{\begin{array}{l}{a-1≤\frac{1}{2}}\\{a+1≥\frac{3}{2}}\end{array}\right.$,解出即可得出.
解答 解:不等式(x-a)2<1,解得:a-1<x<a+1.
不等式(x-a)2<1成立的充分不必要条件是$\frac{1}{2}$<x<$\frac{3}{2}$,
∴$\left\{\begin{array}{l}{a-1≤\frac{1}{2}}\\{a+1≥\frac{3}{2}}\end{array}\right.$,
解得$\frac{1}{2}≤a≤\frac{3}{2}$,
故选:B.
点评 本题考查了不等式的解法、充要条件得的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
17.在锐角△ABC中,已知AB=2,∠B=2∠C,则AC的取值范围是( )
| A. | (2$\sqrt{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{2}$) | C. | (2$\sqrt{2}$,4) | D. | (2,2$\sqrt{3}$) |
14.在等差数列{an}中,若3(a4+a6)+2(a7+a9+a11)=24,则此数列的前13项之和为( )
| A. | 13 | B. | 26 | C. | 52 | D. | 156 |
1. 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
(Ⅰ)完成频率分布表,并画出频率分布直方图;
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | |
| [1.34,1.38) | 25 | |
| [1.38,1.42) | 30 | |
| [1.42,1.46) | 29 | |
| [1.46,1.50) | 10 | |
| [1.50,1.54) | 2 | |
| 合计 | 100 |
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
11.函数$f(x)=\frac{-3+4x}{5-2x}$的值域是( )
| A. | (-∞,2)∪(2,+∞) | B. | (-∞,-2)∪(-2,+∞) | C. | $({-∞,\frac{5}{2}})∪({\frac{5}{2},+∞})$ | D. | R |
18.已知全集U={x||x|≤2},A={x|x2+x-2≤0},则∁UA=( )
| A. | {x|1≤x≤2} | B. | {x|1<x≤2} | C. | {x|-1≤x≤2} | D. | {x|-1<x≤2} |
15.下列说法正确的是( )
| A. | 命题“若幂函数f(x)=xa在(0,+∞)内单调递减,则 a<0”的逆否命题是“若a≥0,则幂函数f(x)=xa在(0,+∞)内单调递增” | |
| B. | 已知命题p 和q,若p∧q为假命题,则命题p、q中必有一个是真命题、一个是假命题 | |
| C. | 若x,y∈R,则“x=y”是“$xy≥{(\frac{x+y}{2})^2}$”的充要条件 | |
| D. | 若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1>0 |
 中,
中,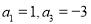 ,则
,则 ____________.
____________.