解不等式|x-1|+|2x+1|＜2．题目和参考答案——青夏教育精英家教网—

题目内容

10．解不等式|x-1|+|2x+1|＜2．

分析把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．

解答解：不等式|x-1|+|2x+1|＜2，等价于$\left\{\begin{array}{l}{x＜-\frac{1}{2}}\\{1-x-2x-1＜2}\end{array}\right.$①，或$\left\{\begin{array}{l}{-\frac{1}{2}≤x＜1}\\{1-x+2x+1＜2}\end{array}\right.$②，或$\left\{\begin{array}{l}{x≥1}\\{x-1+2x+1＜2}\end{array}\right.$③．
解①求得-$\frac{2}{3}$＜x＜-$\frac{1}{2}$，解②求得-$\frac{1}{2}$≤x＜0，解③求得x∈∅．
综上可得，原不等式的解集为{x|-$\frac{2}{3}$＜x＜0}．

点评本题主要考查分式不等式的解法，体现了等价转化和分类讨论的数学思想，属于基础题．

练习册系列答案

相关题目

20．一个几何体的三视图如图所示，则该几何体的体积为（　　）

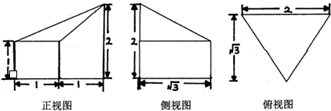
$\frac{4\sqrt{3}}{3}$

D．

2$\sqrt{3}$

1．对于命题：p：?x∈（0，$\frac{π}{2}$），sinx+cosx＞1；q：?x∈R，sin²x+cos²x＞1，则下列判断正确的是（　　）

18．已知各项均为正数的两个数列{a_n}和{b_n}满足：a_n+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}$，b_n+1=1+$\frac{{b}_{n}}{{a}_{n}}$，n∈N^*，
（1）求证：数列{（$\frac{{b}_{n}}{{a}_{n}}$）²}是等差数列；
（2）若a₁=b₁=1，令（$\frac{{b}_{n}}{{a}_{n}}$）²=$\frac{1}{{c}_{n}}$，求证：$\frac{1}{{{c}_{1}}^{2}}$+$\frac{1}{{{c}_{2}}^{2}}$+$\frac{1}{{{c}_{3}}^{2}}$+…+$\frac{1}{{{c}_{n}}^{2}}$＜2．

5．用平面在正方体上截下一个三棱锥，以原来正方体的那个顶点作为三棱锥的顶点，则该顶点在三棱锥的底面上的射影是这个三角形的（　　）

15．在锐角△ABC中，角A、B、C所对的边分别为a、b、c，若2a=b+c，则$\frac{tanA}{tanB}+\frac{tanA}{tanC}$的最大值是2．

2．已知函数f（x）=|x-1|+|x-a|．
（1）若a=2，解不等式f（x）≤2；
（2）若对任意的x∈R，恒有f（x）≥2，求实数a的取值范围．

19．已知函数f（x）=log${\;}_{\frac{1}{2}}$（1-x），g（x）=log${\;}_{\frac{1}{2}}$（1+x）
（1）设函数F（x）=f（x）-g（x），求F（-$\frac{3}{5}$）的值；
（2）若x∈[0，1]，f（m-2x）≤$\frac{1}{2}$g（x）恒成立，求实数m的取值范围．

20．下列关于函数f（x）=-2sin2x-cos4x（x∈R）的说法正确的是（　　）

	A．	f（x）的最小正周期为2π		B．	f（x）的最大值为-1
	C．	f（x）是偶函数		D．	f（x）在[$\frac{π}{12}$，$\frac{π}{4}$]上单调增

试题分类