题目内容
16.设方程x2+ax+b-2=0(a,b∈R)的两根分别在区间(-∞,-2]和[2,∞)上,则a2+b2的最小值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{4}{5}$ | D. | 4 |
分析 方程x2+ax+b-2=0(a,b∈R)的两根分别在区间(-∞,-2]和[2,∞)上,则$\left\{\begin{array}{l}2-2a+b≤0\\ 2+2a+b≤0\end{array}\right.$,画出可行域,并分析目标函数a2+b2的几何意义,可得答案.
解答 解:∵方程x2+ax+b-2=0(a,b∈R)的两根分别在区间(-∞,-2]和[2,∞)上,
∴$\left\{\begin{array}{l}2-2a+b≤0\\ 2+2a+b≤0\end{array}\right.$,
满足条件的可行域如下图所示: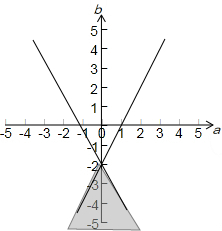
a2+b2表示可行域内点(a,b)到原点距离的平方,
故当a=0,b=2时,a2+b2的最小值是4,
故选:D
点评 本题考查的知识点是二次函数的性质,线性规划,是函数与线性规划的综合应用,难度中档.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
7.根据历年气象资料统计,蚌埠地区五月份刮东风的概率是$\frac{4}{15}$,既刮东风又下雨的概率是$\frac{7}{30}$,那么在“五月份刮东风”的条件下,蚌埠地区五月份下雨的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{2}$ | C. | $\frac{56}{900}$ | D. | $\frac{7}{8}$ |
8.已知集合A={x||x-1|>x-1},B={y|y=lnx},则A∩B=( )
| A. | {x|0<x<1} | B. | {x|x<1} | C. | {x|0<x≤1} | D. | {x|x≤1} |