题目内容
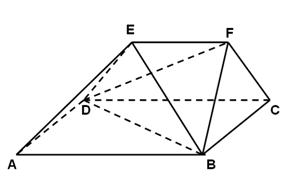
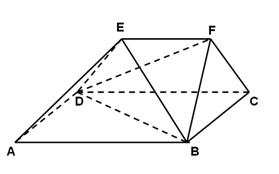
(本小题10分)如图已知在三棱柱ABC——A1B1C1中,AA1⊥面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.

(1) 求证:面PCC1⊥面MNQ;
(2) 求证:PC1∥面MNQ。
【答案】
见解析。
【解析】本试题主要是考查了面面垂直的运用以及线面平行的证明综合运用。
(1)因为AC=BC, P是AB的中点 ∴AB⊥PC ∵AA1⊥面ABC,CC1∥AA1
CC1⊥面ABC而AB在平面ABC内,由此推理得到MN⊥面PCC1即可。
(2)连PB1与MN相交于K,连KQ,∵MN∥PB,N为BB1的中点,∴K为PB1的中点.
又∵Q是C1B1的中点 ∴PC1∥KQ,则由线面平行 的判定定理得到结论。
证明:(1)∵AC=BC, P是AB的中点 ∴AB⊥PC ∵AA1⊥面ABC,CC1∥AA1,
∴CC1⊥面ABC而AB在平面ABC内 ∴CC1⊥AB, ∵CC1∩PC=C ∴AB⊥面PCC1;
又∵M、N分别是AA1、BB1的中点,四边形AA1B1B是平行四边形,MN∥AB,∴MN⊥面PCC1
∵MN在平面MNQ内,∴面PCC1⊥面MNQ;
(2)连PB1与MN相交于K,连KQ,∵MN∥PB,N为BB1的中点,∴K为PB1的中点.
又∵Q是C1B1的中点 ∴PC1∥KQ 而KQ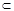 平面MNQ,PC1
平面MNQ,PC1 平面MNQ ∴PC1∥面MNQ.
平面MNQ ∴PC1∥面MNQ.

练习册系列答案
相关题目
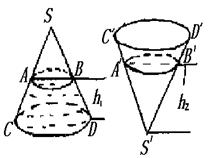
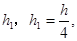 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为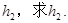

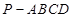 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱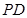 ⊥底面
⊥底面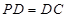 .
.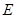 是
是 的中点.(1)证明
的中点.(1)证明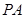 ∥平面
∥平面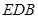 ;(2)证明:
;(2)证明: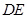 ⊥平面
⊥平面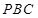 .
.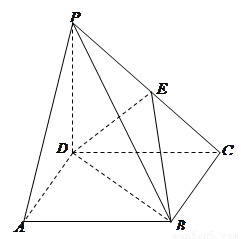
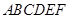 中,四边形
中,四边形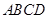 是正方形,
是正方形,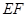 ∥
∥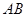 ,
,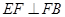 ,
,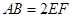 ,
,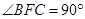 ,
,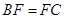 .
.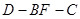 的正切值;
的正切值;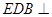 平面
平面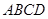 .
.