题目内容
设数列{an}的前n项的和为Sn,满足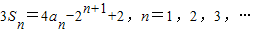
(Ⅰ)求首项a1
(Ⅱ)令
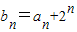 ,求证{bn}是等比数列;
,求证{bn}是等比数列;(Ⅲ)设
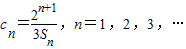 ,数列{cn}的前n项的和为Tn,证明:Tn<1.
,数列{cn}的前n项的和为Tn,证明:Tn<1.
【答案】分析:(Ⅰ)n=1代入,即可求a1;
(Ⅱ)再写一式,两式相减,即可证明{bn}是等比数列;
(Ⅲ)写出数列的通项,利用裂项法求和,即可证得结论.
解答:(Ⅰ)解:当n=1时,3a1=3S1=4a1-4+2,∴a1=2 …(2分)
(Ⅱ)证明:由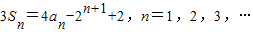 ①
①
则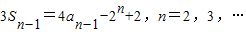 ②
②
将①和②相减得3an=3Sn-3Sn-1=4(an-an-1)-(2n+1-2n)
整理得an=4an-1+2n,…(4分)
故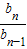 =
=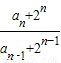 =4(n≥2)
=4(n≥2)
因而数列{bn}是首项为b1=a1+2=4,公比为4的等比数列 …(6分)
(Ⅲ)证明:由(Ⅱ)知bn=4n,
∵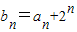 ,∴an=4n-2n,…(7分)
,∴an=4n-2n,…(7分)
将an=4n-2n代入①得 =2(2n+1-1)(2n-1)
=2(2n+1-1)(2n-1)
∴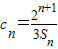 =
=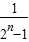 -
-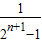 …(12分)
…(12分)
∴Tn= -
-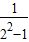 +…+
+…+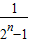 -
-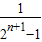 =1-
=1-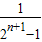 <1 …(14分)
<1 …(14分)
点评:本题考查数列递推式,考查等比数列的证明,考查裂项法求数列的和,确定数列的通项是关键.
(Ⅱ)再写一式,两式相减,即可证明{bn}是等比数列;
(Ⅲ)写出数列的通项,利用裂项法求和,即可证得结论.
解答:(Ⅰ)解:当n=1时,3a1=3S1=4a1-4+2,∴a1=2 …(2分)
(Ⅱ)证明:由
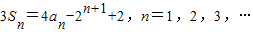 ①
①则
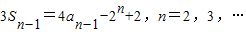 ②
②将①和②相减得3an=3Sn-3Sn-1=4(an-an-1)-(2n+1-2n)
整理得an=4an-1+2n,…(4分)
故
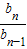 =
=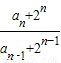 =4(n≥2)
=4(n≥2)因而数列{bn}是首项为b1=a1+2=4,公比为4的等比数列 …(6分)
(Ⅲ)证明:由(Ⅱ)知bn=4n,
∵
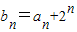 ,∴an=4n-2n,…(7分)
,∴an=4n-2n,…(7分)将an=4n-2n代入①得
 =2(2n+1-1)(2n-1)
=2(2n+1-1)(2n-1)∴
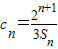 =
=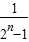 -
-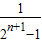 …(12分)
…(12分)∴Tn=
 -
-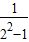 +…+
+…+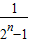 -
-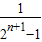 =1-
=1-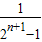 <1 …(14分)
<1 …(14分)点评:本题考查数列递推式,考查等比数列的证明,考查裂项法求数列的和,确定数列的通项是关键.

练习册系列答案
相关题目