题目内容
已知椭圆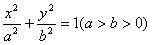 的左右焦点分别为F1,F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=
的左右焦点分别为F1,F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=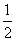 ,
,
(1)求椭圆的标准方程;
(2)若P是椭圆上的任意一点,求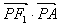 的取值范围;
的取值范围;
(3)直线l:y=kx+m与椭圆相交于不同的两点M,N (均不是长轴的顶点),AH⊥MN垂足为H且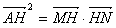 ,求证:直线l恒过定点.
,求证:直线l恒过定点.
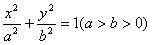 的左右焦点分别为F1,F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=
的左右焦点分别为F1,F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=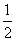 ,
,(1)求椭圆的标准方程;
(2)若P是椭圆上的任意一点,求
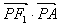 的取值范围;
的取值范围;(3)直线l:y=kx+m与椭圆相交于不同的两点M,N (均不是长轴的顶点),AH⊥MN垂足为H且
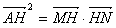 ,求证:直线l恒过定点.
,求证:直线l恒过定点. 解:(1)由题意得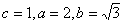 ,
,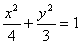 。
。
(2)设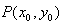 ,
,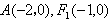 ,
,
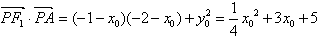 ,
,
由椭圆方程得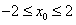 ,二次函数开口向上,对称轴x=-6<-2,
,二次函数开口向上,对称轴x=-6<-2,
当x0=-2时,取最小值0;当x0=2时, 取最大值12,
∴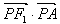 的取值范围是[0,12]。
的取值范围是[0,12]。
(3)由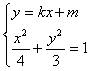 ,得
,得 ,
,
由△>0,得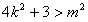 , ※
, ※
设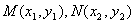 ,则
,则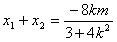 ,
,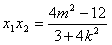 ,
,
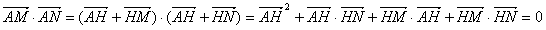 ,
,
∴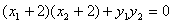 ,
,
即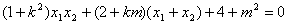 ,
,
∴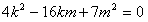 ,∴
,∴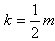 或
或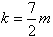 均适合※,
均适合※,
当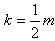 时,直线过A,舍去,故
时,直线过A,舍去,故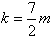 ;
;
当 时,直线
时,直线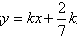 过定点
过定点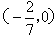 。
。
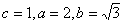 ,
,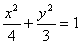 。
。 (2)设
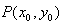 ,
,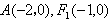 ,
,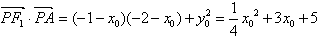 ,
,由椭圆方程得
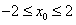 ,二次函数开口向上,对称轴x=-6<-2,
,二次函数开口向上,对称轴x=-6<-2,当x0=-2时,取最小值0;当x0=2时, 取最大值12,
∴
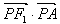 的取值范围是[0,12]。
的取值范围是[0,12]。(3)由
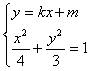 ,得
,得 ,
,由△>0,得
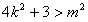 , ※
, ※设
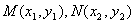 ,则
,则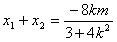 ,
,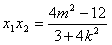 ,
,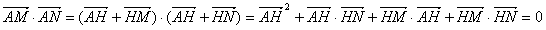 ,
,∴
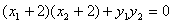 ,
,即
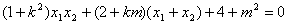 ,
,∴
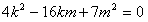 ,∴
,∴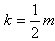 或
或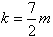 均适合※,
均适合※, 当
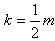 时,直线过A,舍去,故
时,直线过A,舍去,故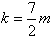 ;
;当
 时,直线
时,直线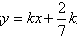 过定点
过定点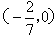 。
。 
练习册系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点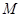 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.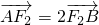 ,求k的值.
,求k的值. 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆