题目内容
 已知椭圆
已知椭圆![]()
![]()
![]() 的左右焦点分别是
的左右焦点分别是![]() ,直线
,直线![]()
![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() 且当
且当![]() 时,M是椭圆
时,M是椭圆![]() 的上顶点,且△
的上顶点,且△![]() 的周长为6.
的周长为6.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左顶点为A,直线
的左顶点为A,直线![]() 与直线:
与直线:![]()
分别相交于点![]() ,问当
,问当![]() 变化时,以线段
变化时,以线段![]() 为直径的圆
为直径的圆
被![]() 轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
解:(1)当![]() 时,直线的倾斜角为
时,直线的倾斜角为![]() ,所以:
,所以: …………3分
…………3分
解得:![]() , …………………………………………………………5分
, …………………………………………………………5分
所以椭圆方程是:![]() ;…………………………………………………………6分
;…………………………………………………………6分
当![]() 时,直线
时,直线![]() 的方程为:
的方程为:![]() ,此时,
,此时,![]() 点的坐标分别是
点的坐标分别是![]() ,又
,又![]() 点坐标是
点坐标是![]() ,由图可以得到
,由图可以得到![]() 两点坐标分别是
两点坐标分别是![]() ,以
,以![]() 为直径的圆过右焦点,被
为直径的圆过右焦点,被![]() 轴截得的弦长为6,猜测当
轴截得的弦长为6,猜测当![]() 变化时,以
变化时,以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,被
,被![]() 轴截得的弦长为定值6,………………………………………………………………8分
轴截得的弦长为定值6,………………………………………………………………8分
证明如下:设点![]() 点的坐标分别是
点的坐标分别是![]() ,则直线
,则直线![]() 的方程是:
的方程是:![]() ,
,
所以点![]() 的坐标是
的坐标是![]() ,同理,点
,同理,点![]() 的坐标是
的坐标是![]() ,…………………9分
,…………………9分
由方程组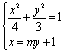 得到:
得到:![]() ,
,
所以:![]() ,………………………………………11分
,………………………………………11分
从而:![]()
![]() =0,
=0,
所以:以![]() 为直径的圆一定过右焦点
为直径的圆一定过右焦点![]() ,被
,被![]() 轴截得的弦长为定值6。……………13分
轴截得的弦长为定值6。……………13分

练习册系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点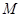 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.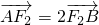 ,求k的值.
,求k的值. 已知椭圆
已知椭圆 已知椭圆
已知椭圆