题目内容
9、f(x)=ax2+ax-1在R上满足f(x)<0恒成立,则a的取值范围是( )
分析:分三种情况讨论:(1)当a等于0时,原不等式变为-1小于0,显然成立;
(2)当a大于0时,根据二次函数的图象与性质可知解集为R不可能;
(3)当a小于0时,二次函数开口向下,且与x轴没有交点即△小于0时,函数值y恒小于0,即解集为R成立,根据△小于0列出不等式,求出a的范围,综上,得到满足题意的a的范围.
(2)当a大于0时,根据二次函数的图象与性质可知解集为R不可能;
(3)当a小于0时,二次函数开口向下,且与x轴没有交点即△小于0时,函数值y恒小于0,即解集为R成立,根据△小于0列出不等式,求出a的范围,综上,得到满足题意的a的范围.
解答:解:(1)当a=0时,得到4>0,显然不等式的解集为R;
(2)当a<0时,二次函数y=ax2+ax-1开口向下,由不等式的解集为R,得到二次函数与x轴没有交点即△=a2+4a<0,即a(a+4)<0,
解得-4<a<0;
(3)当a>0时,二次函数y=ax2+ax-1开口向上,函数值y不恒<0,故解集为R不可能.
综上,a的取值范围为(-4,0]
故选D.
(2)当a<0时,二次函数y=ax2+ax-1开口向下,由不等式的解集为R,得到二次函数与x轴没有交点即△=a2+4a<0,即a(a+4)<0,
解得-4<a<0;
(3)当a>0时,二次函数y=ax2+ax-1开口向上,函数值y不恒<0,故解集为R不可能.
综上,a的取值范围为(-4,0]
故选D.
点评:本题考查一元二次不等式的解法,考查分类讨论及函数的思想,是中档题.

练习册系列答案
相关题目
 ≥2在x∈[1,2]上恒成立,求实数a的取值范围;
≥2在x∈[1,2]上恒成立,求实数a的取值范围;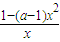 在(2,3)上是增函数,求实数a的取值范围.
在(2,3)上是增函数,求实数a的取值范围.