题目内容
已知函数f(x)=ax2+a(x>0)的图象恒在直线y=-2x的下方,则实数a的取值范围是( )A.(-∞,-1)
B.(-1,0)∪(0,+∞)
C.(-∞,0)
D.(-∞,-1)∪(1,+∞)
【答案】分析:把恒成立问题等价转化,利用导数即可得出a的取值范围.
解答:解:由题意可得:当x>0时,-2x-(ax2+a)>0恒成立.
即x∈(0,+∞)时,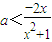 恒成立?
恒成立?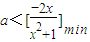 ,x∈(0,+∞).
,x∈(0,+∞).
令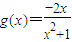 ,x∈(0,+∞),则
,x∈(0,+∞),则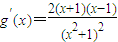 ,
,
令g′(x)=0,则x=1.
当x>1时,g′(x)>0,函数g(x)单调递增;当0<x<1时,g′(x)<0,函数g(x)单调递减.
∴当x=1时,函数g(x)取得极小值g(1)=-1,也是最小值.
∴a<-1.
因此a的取值范围是(-∞,-1).
故选A.
点评:正确把恒成立问题等价转化,熟练掌握利用导数求函数的极值最值是解题的关键.
解答:解:由题意可得:当x>0时,-2x-(ax2+a)>0恒成立.
即x∈(0,+∞)时,
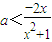 恒成立?
恒成立?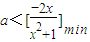 ,x∈(0,+∞).
,x∈(0,+∞).令
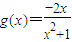 ,x∈(0,+∞),则
,x∈(0,+∞),则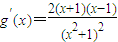 ,
,令g′(x)=0,则x=1.
当x>1时,g′(x)>0,函数g(x)单调递增;当0<x<1时,g′(x)<0,函数g(x)单调递减.
∴当x=1时,函数g(x)取得极小值g(1)=-1,也是最小值.
∴a<-1.
因此a的取值范围是(-∞,-1).
故选A.
点评:正确把恒成立问题等价转化,熟练掌握利用导数求函数的极值最值是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目